Recognition of Biclique Graphs of Some Graph Classes

There is a PDF version (with references) that can be accessed here.

Table 1: Biclique graph of some classes. At column ``\(KB(G)\), \(G \in \mathcal{A}\)'' we can find a brief description of the graph \(KB(G)\) for each class; at column ``class \(KB(\mathcal{A})\)'' appears the class that is equal to (or a super-class of) \(KB(\mathcal{A})\). At column ``complexity'' we present the complexity (if known) of recognizing \(KB(\mathcal{A})\).
class \(\mathcal{A}\)	\(KB(G)\), \(G \in \mathcal{A}\)	class \(KB(\mathcal{A})\)	complexity
complete	\(L(G)\) \cite{CruzGroshausGuedesPuppo2020}	\(L(\text{complete})\) \cite{CruzGroshausGuedesPuppo2020}	\(\mathcal{P}\) \cite{Lehot1974,Liu2015,Roussopoulos1973}
tree	\((G-leaves(G))^2\) \cite{CruzGroshausGuedesPuppo2020}	\((\text{tree})^2\) \cite{CruzGroshausGuedesPuppo2020}	\(\mathcal{P}\) (linear) \cite{LinSkiena1995}
path (\(P_n\))	\(\emptyset\), for \(n = 1\)	\((\text{path})^2\) \cite{CruzGroshausGuedesPuppo2020}	\(\mathcal{P}\) (linear) \cite{LinSkiena1995}
	\(K_1\), for \(n = 2\)
	\((P_{n-2})^2\), for \(n > 2\)
	\cite{CruzGroshausGuedesPuppo2020}
half (with \(2n\) vertices) \cite{Erdos1983}	\(K_n\)	complete	\(\mathcal{P}\) (linear)
star	\(K_1\)	\(K_1\)	\(\mathcal{P}\) (constant)
bistar	\(K_2\)	\(K_2\)	\(\mathcal{P}\) (constant)
\((K_3,P_4)\text{-free}\) graphs	\(\mathcal{C}_{>1}(G) K_1\)	\(n K_1\) \cite{Cruz2024,CruzGroshausGuedesProcedia2023}	\(\mathcal{P}\) (constant)
\((K_3,\text{co-}P_3)\text{-free}\) graphs	\(K_1\)	\(K_1\)	\(\mathcal{P}\) (constant)
caterpilar	\((G-leaves(G))^2\)	\((\text{path})^2\)	\(\mathcal{P}\) (linear) \cite{LinSkiena1995}
cycle (\(C_n\))	\(K_1\), for \(n = 4\)	\((\text{cycle})^2 - K_4 + K_1\)	\(\mathcal{P}\) \cite{FarzadLauLeTuy2012}
	\((C_n)^2\), for \(n \neq 4\) \cite{CruzGroshausGuedesPuppo2020}	\cite{CruzGroshausGuedesPuppo2020}
\(\mathcal{G}_k\), for \(k \geq 5\)	\((G-leaves(G))^2\)	\((\mathcal{G}_k)^2\), for \(k \geq 5\)	\(\mathcal{P}\), for \(k \geq 6\)
	\cite{CruzGroshausGuedesPuppo2020}	\cite{CruzGroshausGuedesPuppo2020}	\(\mathcal{NP}\text{-complete}\), for \(k = 5\)
			\cite{FarzadLauLeTuy2012}
\(ICB\)	OPEN	\(\subset (IIC-PG)^2\) \cite{Cruz2024,CruzGroshausGuedesProcedia2023,CruzGroshausGuedes2022MC}	*
\(IBG\)	OPEN	\(\subset (IIC-PG)^2\) \cite{Cruz2024,CruzGroshausGuedesProcedia2023}	OPEN
		\(\subset K_{1,4}\text{-free co-}CG\) \cite{CruzGroshausGuedesPuppo2020}
\(PIB\)	\((L(S(G))^2\) \cite{CruzGroshausGuedesPuppo2020}	\((L(PIB))^2\) \cite{CruzGroshausGuedesPuppo2020}	OPEN
\(PIB\text{-}ASG\)	\((L(S(G))^2\) \cite{CruzGroshausGuedesPuppo2020}	\(1\text{-}PIG\) \cite{CruzGroshausGuedesPuppo2020}	\(\mathcal{P}\) \cite{CruzGroshausGuedesPuppo2020}
\(HIB\)	\(K(G^2)\) \cite{Groshaus2006}	\(\subset PIG \cap (L(PIB))^2\)	OPEN
		\cite{CruzGroshausGuedesPuppo2020,GroshausGuedesKolbergLATIN2020,Groshaus2008,Hedman1984}
\((K_3,C_5,C_6,P_6)\text{-free}\) graphs	\(K(G^2)\) \cite{Groshaus2006}	---	OPEN
\(DFCB\)	\(K(G^2)\) \cite{Groshaus2006}	\(\subset\) Dually Chordal	OPEN
\(HONHG\)	\(K(G^2)\) \cite{Groshaus2006}	---	OPEN
\(BBHGD\)	OPEN	\(CHBDI\) \cite{Groshaus2006}	OPEN
\(NSSG\)	---	---	\(\mathcal{P}\) \cite{GroshausGuedesPuppo2016,GroshausGuedesPuppo2022}
threshold graphs	---	---	\(\mathcal{P}\) \cite{GroshausGuedesPuppo2016,GroshausGuedesPuppo2022}
\(K_3\text{-free}\) graphs	\((KB_m(G))^2\) \cite{GroshausGuedes2020,GroshausGuedesProcedia2021}	\(\subset \mathcal{G}^2\) \cite{GroshausGuedes2020,GroshausGuedesProcedia2021}	OPEN
\(bipartite\)	\((KB_m(G))^2\) \cite{GroshausGuedes2020,GroshausGuedesProcedia2021}	\((IIC\text{-comparability})^2\)	OPEN
		\cite{GroshausGuedes2020,GroshausGuedesProcedia2021}
		Characterization \cite{Groshaus2006}
\(\mathcal{G}\)	---	Characterization \cite{Groshaus2006}	OPEN

Figure of graph classes inclusions

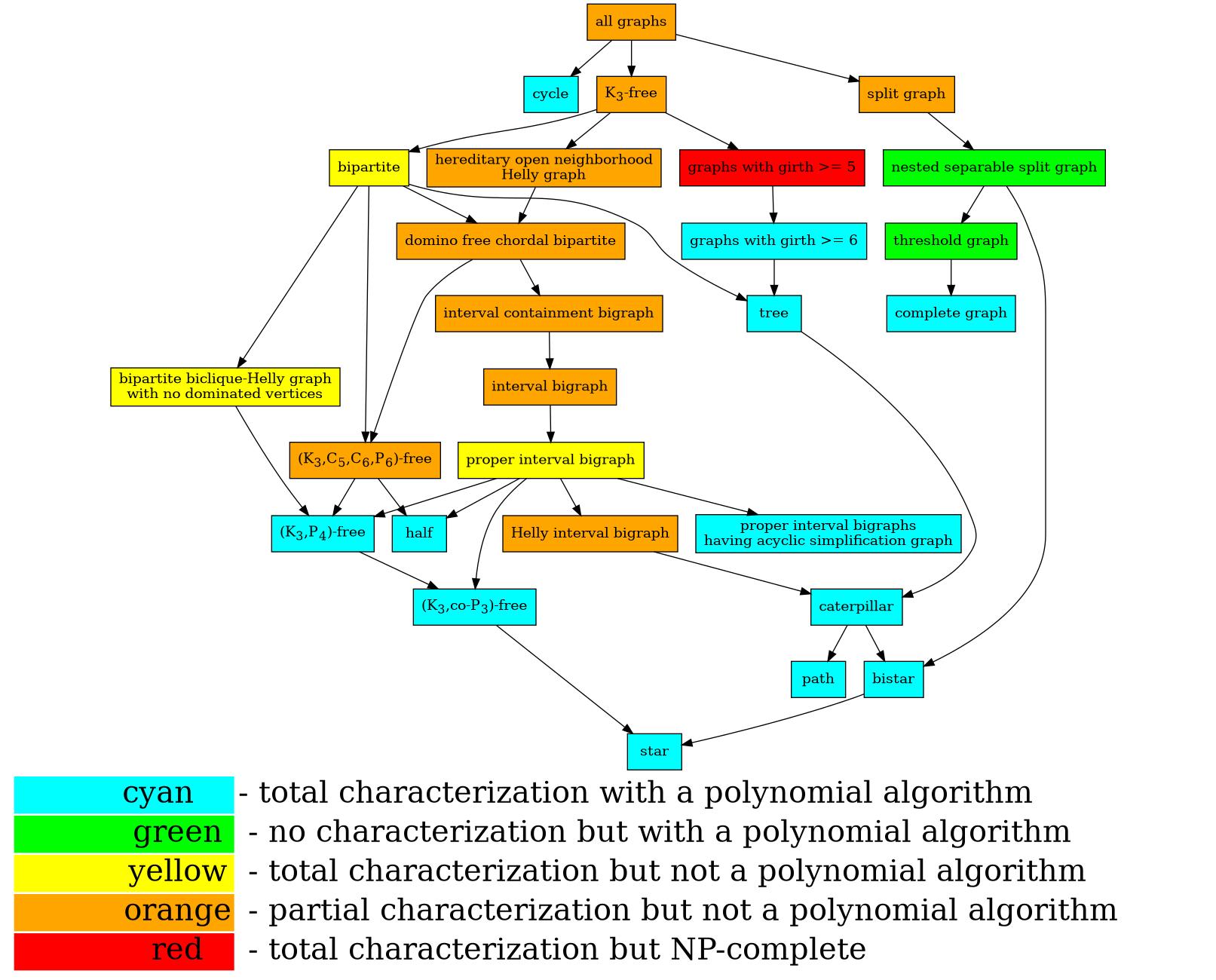
Figure 1: Graph classes and the status of the recognition of its biclique graph

Glossary

Classes

\(BBHGD\): Bipartite biclique-Helly graphs with no dominated vertices \cite{Groshaus2006}
\(BPG\): Bipartite permutation graphs \cite{Spinrad1987} (\(= PIB\) \cite{HellHuang2004})
\(CHBDI\): Clique independent Helly-bicovered with no dominated vertices graphs \cite{Groshaus2006}
co-\(CG\): Co-comparability graphs
\(C_n\): Cycle with \(n\) vertices
\(DFCB\): Domino-free Chordal Bipartite \cite{Groshaus2006}
\(\mathcal{G}\): All graphs
\(\mathcal{G}_k\): Graphs with girth at least \(k\)
\(HIB\): Helly interval bigraphs \cite{GroshausGuedesKolbergLATIN2020}
\(HONHG\): Hereditary open neighborhood Helly graphs (\(= (K_3,C_6)\text{-free}\) graphs) \cite{Groshaus2006}
\(IBG\): Interval bigraphs \cite{HellHuang2004}
\(ICB\): Interval containment bigraphs
\(IIC\text{-comparability}\): Interval intersection closed comparability graphs \cite{GroshausGuedes2020,GroshausGuedesProcedia2021}
\(K_n\): Complete graph of order \(n\)
\(NSSG\): Nested separable split graphs \cite{GroshausGuedesPuppo2016,GroshausGuedesPuppo2022}
\(PG\): Permutation Graphs
\(PIB\): Proper interval bigraphs (\(= BPG\) \cite{HellHuang2004})
\(PIB\text{-}ASG\): Proper interval bigraphs having acyclic simplification graph \cite{CruzGroshausGuedesPuppo2020}
\(PIG\): Proper interval graphs
\(1\text{-}PIG\): \(1\text{-Proper}\) interval graphs \cite{CruzGroshausGuedesPuppo2020}
\(P_n\): Path with \(n\) vertices

Operators and Functions

\(\mathcal{C}_{>1}(G)\): Number of non-trivial components of \(G\)
\(K(G)\): Clique graph of \(G\)
\(L(G)\): Line graph of graph \(G\)
\(leaves(G)\): Set of leaves (vertices of degree \(1\)) of graph \(G\)
\(S(G)\): Simplification graph of \(G\) \cite{CruzGroshausGuedesPuppo2020}