Agradecimentos
Primeiramente gostaria de agradecer aos meus pais pela formação que eles me deram. O que proporcionou, apesar das dificuldades, concluir a universidade. Gostaria de agradecer também a minha namorada Gizelle Marques pelo incentivo, motivação e carinho sempre nos momentos certos. Agradeço também ao Oliver Matias van Kaick que mesmo fazendo doutorado no Canada foi prestativo em responder dúvidas e em dar dicas para que eu pudesse iniciar o trabalho com o GRAFO. E por final agradeço ao professor André Luiz Pires Guedes por ter aceitado realizar a minha orientação mesmo não tendo realizado orientação do meu trabalho de graduação I.
Esse documento tem a intenção de ser um tutorial para se trabalhar com o GRAFO - graph editor. O GRAFO é uma ferramenta de ensino e de testes para trabalhos com grafos. Ele proporciona a construção, edição, manipulação de grafos e testes de algoritmos. Através da sua interface de plugins pode-se facilmente construir um novo algoritmo e testa-lo. O usuário não precisa se preocupar com a interface gráfica, esta é fornecida pelo GRAFO. Com isso ganha-se em tempo e produtividade. Também neste trabalho foi introduzido a possibilidade de construção de algoritmos passo a passo. Esta funcionalidade fornece ao usuário a possibilidade de interagir e depurar os algoritmos por ele construídos.
O GRAFO surgiu em 2003 com uma idéia de Murilo Vicente Goncalves da Silva de construir um programa que facilitasse os testes de algoritmos. A primeira versão do programa possuía uma interface OpenGL e alguns poucos algoritmos nativos.
Algum tempo depois a idéia foi encampada por Oliver Matias van Kaick. Nesta época o Murilo Vicente e o Oliver Matias eram do PET (Programa de Educação Tutorial) do curso de Ciência da computação da UFPR (Universidade Federal do Paraná). A dedicação dos dois somadas a tutoria e experiência do professor André Luiz Pires Guedes permiti-os a construção de toda base que existe atualmente: Interface GTK e OpenGL, comunicação com o GraphViz, utilização de plugins, diferentes layouts para desenho de grafos, rótulos e pesos em vértices e arestas, entre outros.
Em 2008, motivado por esse trabalho e junto com o professor André Guedes decidimos colocar o GRAFO de novo em ação realizando algumas manutenções e implementando as estruturas que possibilitassem a execução de algoritmos Passo a Passo. Entretanto as primeiras investigações sobre o GRAFO abriram outras possibilidades até então não exploradas que se refletem na parte de documentação que também está sendo coberta por este trabalho.
O que veremos nos próximos capítulos dará ao leitor uma noção de teoria de grafos, um detalhamento da interface e funcionalidades e um HowTo - Como Fazer para construir plugins e implementar algoritmos passo a passo. Além disso esta documentação serve como ponto de referência para futuras manutenção e ou implementações nas funcionalidades do GRAFO.
Este trabalho está organizado em 7 capítulos:
Neste capítulo será dada uma breve introdução sobre teoria dos grafos. Essa introdução tem por objetivo contextualizar o leitor para trabalhar com a nomenclatura utilizada no GRAFO.
Tanto em matemática quanto em ciência da computação, a teoria dos grafos estuda a estrutura matemática grafo que são utilizados para modelar a relação entre objetos de uma certa coleção. Neste contexto um grafo é uma coleção de vértices (nodos) e arestas conectando um par de vértices. WIKIPEDIA (2008).
Segundo GAGNON (2001) e SZWARCFITER (1984) um grafo G é um par ordenado G = (V, E) que está sujeito as seguintes condições:
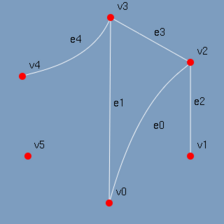
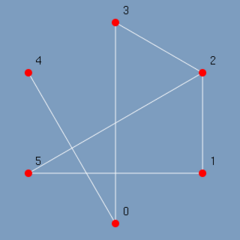
A figura 2.1 traz a representação gráfica do grafo G acima, onde, G = ({v0, v1, v2, v3, v4, v5}, {(v0, v3), (v0, v2), (v0, v3), (v1, v2), (v2, v3), (v3, v4)}).
Os seus vértices correspondem a pontos distintos do plano em posição aleatória e suas arestas correspondem a retas ou curvas que unem estes pontos. SZWARCFITER (1984).

(figura 2.1)
Uma aresta incide aos dois vértices que conecta. Um vértice é incidente a uma aresta a ele conectada. O grau de um vértice é dado pelo número de arestas incidentes a ele. SZWARCFITER (1984). Na figura 2.1 temos como grau dos vértices o seguinte: v0 = 2, v1 = 1, v2 = 3, v3 = 3, v4 = 1, v5 = 0.
Os vértices adjacentes são vértices unidos por uma aresta, na figura 2.1 os pares de vértices não ordenados (v0, v2), (v0, v3), (v1, v2), (v2, v3) e (v3, v4) são adjacentes. Duas arestas são adjacentes quando compartilham um mesmo vértice. No exemplo os pares de arestas não ordenadas (e0, e1), (e0, e2), (e0, e3), (e1, e3), (e1, e4), (e2, e3) e (e3, e4) são adjacentes.
Peso é um valor associado a vértices e arestas de um grafo. Por exemplo um custo, uma distância, uma capacidade ou algo que mensure ir de um vértice a outro utilizando uma determinada aresta ou passando por um determinado vértice. SZWARCFITER (1984).
É denominado caminho em um grafo uma seqüencia de vértices onde para cada vértice existe uma aresta que o conecta ao vértice seguinte. Um caminho de K vértices possui um caminho de comprimento K-1. Se os vértices do caminho não se repetirem a seqüencia recebe o nome de caminho simples. Se as arestas forem únicas a seqüencia recebe o nome de trajeto. Um ciclo é um caminho que começa em um vértice e retorna ao mesmo vértice. SZWARCFITER (1984).
Neste tópico serão exemplificado alguns tipos de grafos citados na interface do GRAFO. São eles: Grafo completo, Grafo bipartite, Grafo regular, Grafo estrela.
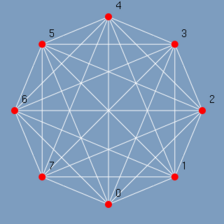
Em um grafo completo todo par de vértice é ligado por uma aresta, isto significa que o grafo possui o máximo de arestas possíveis. GAGNON (2001).
Um grafo com n vértices é nomeado Kn. K1 um grafo com um único vértice e chamado trivial. K2 é um grafo com 2 vértices e uma aresta. K3 é um grafo com 3 vértices e 3 arestas e assim sucessivamente. O número de arestas de um grafo completo é dado por n(n-1)/2.
A figura 2.2 traz o exemplo de um K8 que é um grafo com 8 vértices e 28 arestas.
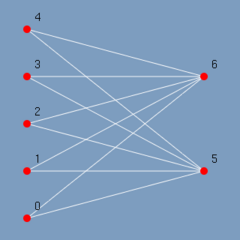
Em um grafo bipartite os vértices são divididos em dois grupos. Sendo que cada vértice do primeiro grupo é adjacente a somente vértices do segundo grupo e vice-versa. De uma maneira mais formal em um grafo bipartite não existe ciclo de comprimento ímpar. SZWARCFITER (1984).
A figura 2.3 traz um exemplo de um grafo bipartite com 5 vértices no primeiro grupo e 3 vértices no segundo.
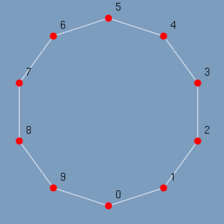
É denominado um grafo regular um grafo onde todos os vértice tem o mesmo grau. Como no exemplo da figura 2.4 que traz um grafo regular com 10 vértices e onde todos os vértices possuem grau 2. GAGNON (2001).
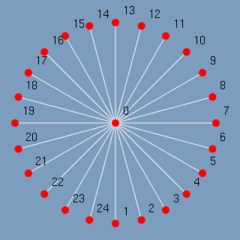
Um grafo estrela é um grafo onde existe um vértice central que é adjacente a todos os outros vértices do grafo. Como na figura 2.5.
 |
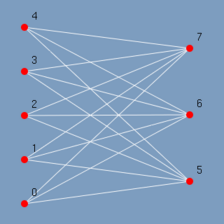 |
| (figura 2.2) | (figura 2.3) |
 |
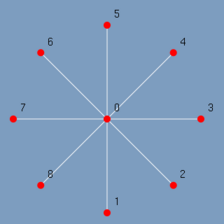 |
| (figura 2.4) | (figura 2.5) |
Neste tópico será abordado uma das maneiras de se representar um grafo em um computador. Esta não é a única maneira de representação de um grafo, porem, é a maneira utilizada internamente pelo GRAFO. Por GAGNON (2001) e SZWARCFITER (1984).
Dado o grafo G = (V, E) de n vértices v0, v1, v2..vn a matriz de adjacências M = (mjk) é uma matriz n x n sujeito as seguintes condições:
| -- | v0 | v1 | v2 | v3 | v4 | v5 |
| v0 | 0 | 0 | 1 | 1 | 0 | 0 |
| v1 | 0 | 0 | 1 | 0 | 0 | 0 |
| v2 | 1 | 1 | 0 | 1 | 0 | 0 |
| v3 | 1 | 0 | 1 | 0 | 1 | 0 |
| v4 | 0 | 0 | 0 | 1 | 0 | 0 |
| v5 | 0 | 0 | 0 | 0 | 0 | 0 |
(tabela 2.1)
Neste capitulo será detalhado a interface que o GRAFO provem ao seu usuário, como menus, botões, opções, configurações e tudo que possa sofrer a interação do usuário. A expansão desta interface, com a criação de novos plugins, será abordada nos capítulos 4 e 5.
A interface do grafo, figura 3.1, possui quatro divisões básicas. São elas:
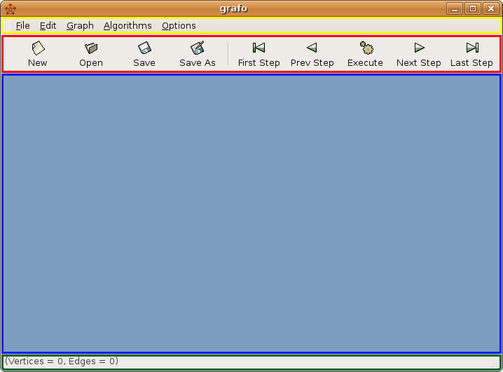 (figura 3.1)
(figura 3.1)
Os menus do GRAFO são divididos em cinco categorias: File, Edit, Graph, Algorithms e Options. Estas por sua vez estão subdivididas de maneira a conter operações correlatas.
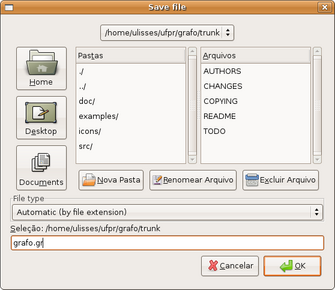
Esta opção de menu, figura 3.2, contém as operações de entrada e saída para o GRAFO.
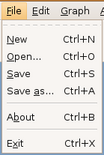
(figura 3.2)
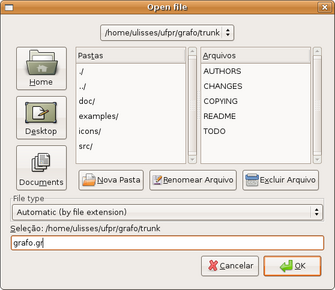 (figura 3.3)
Para maiores detalhes sobre o formato de arquivo GraphViz visite o site (http://www.graphviz.org/).
(figura 3.3)
Para maiores detalhes sobre o formato de arquivo GraphViz visite o site (http://www.graphviz.org/).
 (figura 3.4)
(figura 3.4)
 (figura 3.5)
(figura 3.5)
Esta opção de menu contem as operações para construção de um grafo e a edição de atributos e propriedades. Figura 3.6.
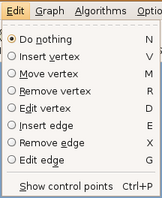
(figura 3.6)
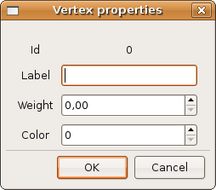 |
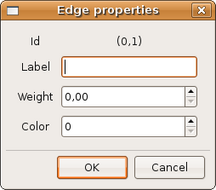 |
| (figura 3.7) | (figura 3.8) |
 |
 |
| (figura 3.9) | (figura 3.10) |
Esta opção de menu oferece manipulações sobre o grafo já construído através do menu Edit. Também traz um wizard para geração de novos grafos e opções para redesenhar grafo em edição com um novo layout. A figura 3.11 traz o menu de opções.
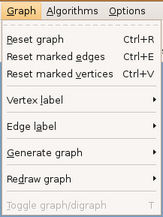
(figura 3.11)
Limpa as estruturas internas e a área de trabalho preparando o ambiente do GRAFO para uma nova edição.
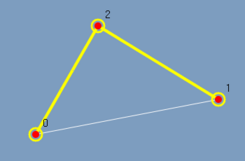
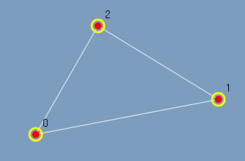
Limpa as arestas destacadas. Como exemplo temos a figura 3.13 quando executado o Reset marked edges sobre o grafo da figura 3.12.
Limpa os vertices destacados. Como exemplo temos a figura 3.14 quando executado o Resete marked vertices sobre o grafo da figura 3.13.
 |
 |
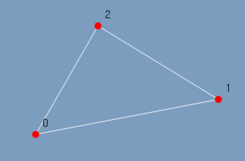 |
| (figura 3.12) | (figura 3.13) | (figura 3.14) |
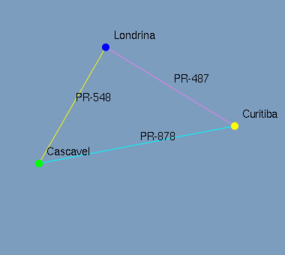
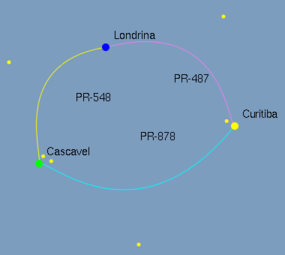
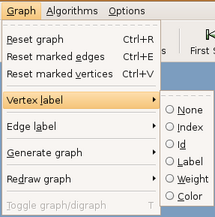
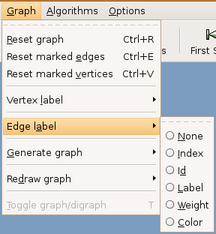
Exibe os vértices nomeados de acordo com a opção selecionada. Figura 3.15. Nas figuras 3.9 e 3.10 foram utilizadas a opção de exibição de label ou rótulos nos vértices. Estes vértices representam as cidades Londrina, Curitiba, Cascavel.
Exibe as arestas nomeadas de acordo com a opção selecionada. Figura 3.16. Nas figuras 3.9 e 3.10 foram utilizadas a opção de exibição de label ou rótulos nas arestas. Estas arestas representam nomes de rodovias, PR-487, PR-548 e PR-878, que ligam as cidades.
 |
 |
| (figura 3.15) | (figura 3.16) |
Gera grafos pré determinados de acordo com um conjunto de parâmetros informados. A figura 3.17 mostra o menu de opções.
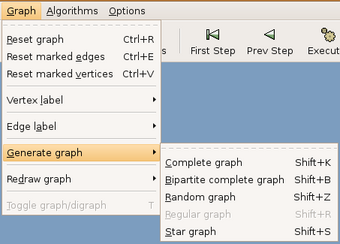
(figura 3.17)
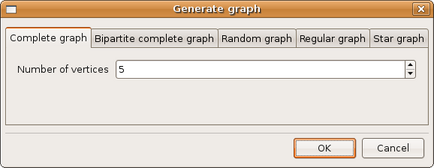 (figura 3.18)
(figura 3.18)
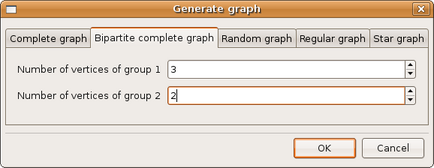 (figura 3.19)
(figura 3.19)
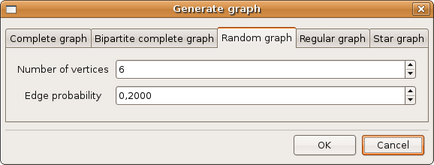 (figura 3.20)
(figura 3.20)
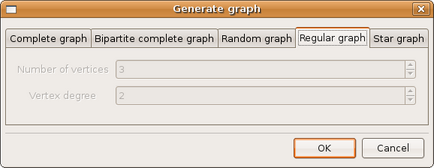 (figura 3.21)
(figura 3.21)
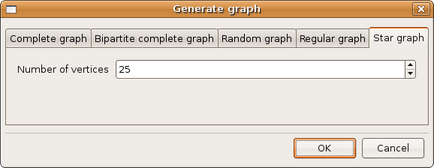 (figura 3.22)
(figura 3.22)
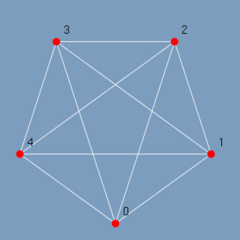 |
 |
| (figura 3.23) | (figura 3.24) |
 |
 |
| (figura 3.25) | (figura 3.26) |
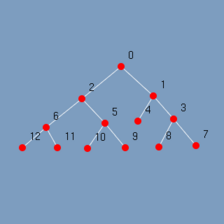
Redesenha o grafo em um novo layout porem mantendo inalterado o seu conjunto de vértices e arestas.
 |
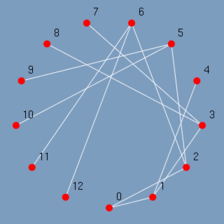 |
| (figura 3.27) | (figura 3.28) |
Altera o tipo do grafo entre Grafo e Digrafo. Esta opção está desabilitada no menu por não estar implementada. No capítulo 6 será abordada a possibilidade de finalização ao suporte a digrafos.
Esta opção de menu, figura 3.29, exibe o elenco de algoritmos disponíveis para utilização no GRAFO.
Os algoritmos estão distribuídos nas categorias de Teste, Resultado, Passo a Passo, Transformação e Busca.
O GRAFO possui algoritmos nativos ou fornecidos através de plugins. Os algoritmos
disponibilizados através de plugins são uma expansão da interface e estão destacados com ícone de plug
( ![]() ).
).
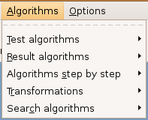
(figura 3.29)
Este menu agrupa as preferências do usuário, configurações, informações sobre plugins e modo de visualização
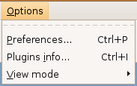
(figura 3.30)
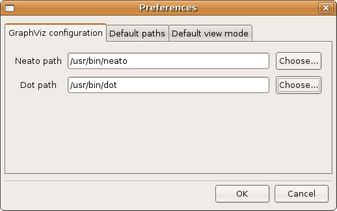 (figura 3.31)
(figura 3.31)
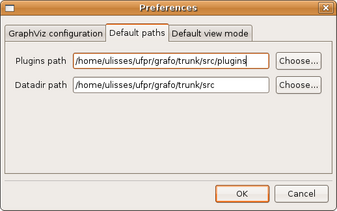 (figura 3.32)
(figura 3.32)
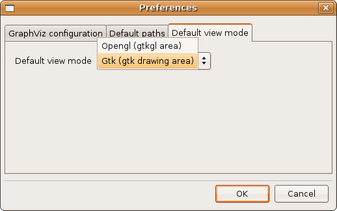 (figura 3.33)
(figura 3.33)
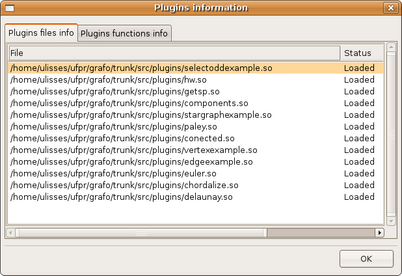 (figura 3.34)
(figura 3.34)
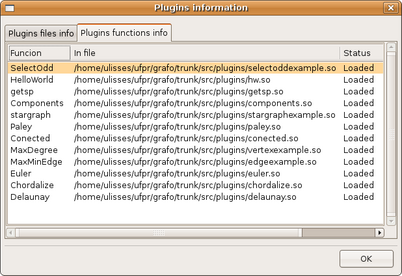 (figura 3.35)
(figura 3.35)
A barra de ferramentas, figura 3.36, traz os comandos básicos de entrada e saída e opções para a manipulação dos algoritmos passo a passo. A utilização dos botões do passo a passo serão detalhadas no capitulo 5.

(figura 3.36)
É na área de trabalho que o usuário edita os seus grafos, recebe o resultado de execução dos algoritmos como o destaque de vértices e arestas e a criação e exclusão de componentes do grafo.
A barra de status serve como canal de comunicação entre o GRAFO e o usuário. É nela que o GRAFO dá instruções, mostra resultados e interage de forma escrita com o usuário. Como por exemplo a figura 3.37 onde o usuário é instruído a clicar na área de trabalho para criar um vértice. Na figura 3.38 o usuário é instruído a clicar em um vértice e arrasta-lo para que este seja movido. E na figura 3.39 o usuário é informado que o grafo por ele escolhido não é cordal.

(figura 3.37)

(figura 3.38)

(figura 3.39)
Este capítulo é um tutorial prático para construção de plugins. Ele começa explorando os headers e estruturas internas ao GRAFO que precisão ser conhecidas antes da construção. Depois através de um exemplo simples, Hello World, é explorado a estrutura de um plugin: headers necessários, protótipo das funções e corpo das funções. Utilizando-se do Hello World também é abordo compilação, instalação e execução de um plugin. O capitulo termina detalhando através do exemplo Get some parameter como se faz para receber parâmetros. Pelo exemplo Generate Star Graph como se cria vértices e arestas. E finalmente utilizando-se dos plugins Highest Degree e Some Edge como se faz respectivamente para destacar os vértices e arestas na interface do grafo.
Os plugins são bibliotecas carregadas dinamicamente pelo GRAFO no momento da inicialização. Cada plugin pode ter um ou mais algoritmos. A cada algoritmo criado recebe uma nova entrada no menu Algorithms de acordo com a sua categoria. São elas:
Sem dúvida a construção de plugins é que torna o GRAFO realmente poderoso. Com eles pode-se facilmente implementar um novo algoritmo e acompanhar visualmente o seu resultado.
Para a construção de plugins é preciso conhecer algumas estruturas internas do GRAFO e os headers onde estão declaradas. São Elas:
graph.h
No header graph.h estão declaradas as estruturas que representam um vértice, uma aresta e um grafo dentro do ambiente. Bem como as funções utilizadas para manipula-los.
Vertex struct - Estrutura de um vértice
A estrutura Vertex (tabela 4.1) contém as informações necessárias para a representação de um vértice são elas: Identificador, nome dado ao vértice, o seu peso, a sua posição (x,y) no plano cartesiano, sua cor, informações se o vértice está conectado, se está marcado, grau do vértice, grau de entrada e grau de saída.
Obs.: A propriedade degree só é utilizada em grafos enquanto que propriedades indegree e outdegree em Digrafos.
| Nome | Tipo | Descrição |
|---|---|---|
id |
int |
Identificador auto incremental e único |
label |
char * |
Texto (nome) associado ao vértice |
weight |
Weight |
Peso da aresta - typedef float |
x |
float |
Posição X em 2D |
y |
float |
Posição Y em 2D |
color |
Color |
Cor do vértice - typedef int |
concomp |
int |
Se 1 o vértice está conectado |
mark |
char |
Se 1 o vértice está marcado |
degree |
int |
Grau do vértice |
indegree |
int |
Grau de entrada |
outdegree |
int |
Grau de saída |
(tabela 4.1)
Edge - Matriz de adjacência
Um aresta é representada pela matriz de adjacência e sua unidade básica é typedef char Edge.
Neste caso assume 0 (zero) ou 1 (um). Na tabela 4.3 onde descrito as propriedades
de um grafo pode ser visto que o Edge é declarado como Edge **, ou seja uma matriz
bidimensional.
Edge_prop struct - Estrutura das propriedades de uma aresta
A estrutura Edge_prop (tabela 4.2) vem complementar a matriz de adjacência Edge. As informações complementares são: Nome associado a aresta, o seu peso, a sua cor, informações se a aresta está marcada e os pontos de controle utilizados para gerar arestas curvas.
| Nome | Tipo | Descrição |
|---|---|---|
label |
char * |
Texto (nome) associado a aresta |
weight |
Weight |
Peso da aresta - typedef float |
color |
Color |
Cor da aresta - typedef int |
mark |
char |
Se 1 a aresta está marcada |
ctrlpoints |
float [4][3] |
Pontos de controle |
(tabela 4.2)
Graph struct - Estrutura de um grafo
A estrutura Graph (tabela 4.3) contém as informações necessárias para a representação de um grafo. São elas: O seu tipo, a quantidade de vértices, o identificador do próximo vértice, a quantidade de vértices para o tipo grafo, a quantidade de arestas para o tipo digrafo, o espaço em memória alocado, a lista de vértices, a matriz de adjacência, a matriz de propriedade dos vértices, o número de componentes conexos e o número de cores utilizadas.
Obs.: As propriedades ncomp, ncolor e encolor não são inicializadas ou atualizadas automaticamente. Caso deseje utiliza-las é necessário que as faça manualmente.
| Nome | Tipo | Descrição |
|---|---|---|
type |
GraphType |
Informa o tipo do grafo - typedef enum (GRAPH,DIGRAPH) |
size |
int |
Quantidade de vértices do grafo |
nextid |
int |
Identificador a ser recebido pelo próximo vértice |
nedges |
int |
Quantidade de vértices (Grafos) |
narcs |
int |
Quantidade de arcos (Digrafos) |
allocated_size |
int |
Espaço alocado |
vertex |
Vertex * |
Lista de vértices |
edge |
Edge ** |
Matriz de adjacência - typedef char |
prop |
Edge_prop ** |
Propriedades da matriz de adjacência |
ncomp |
int |
Número de componentes conexos |
ncolor |
int |
Número de cores utilizadas (Não é número cromático) |
encolor |
int |
Número de cores utilizadas pelas arestas |
(tabela 4.3)
SEdge struct - Estrutura de uma aresta simples
A estrutura SEdge (tabela 4.4) contem a informação do par ordenado que forma uma aresta. Esta estrutura será e incluída será utilizada na lista de destaque de aresta. Vide tabela 4.18 para maiores detalhes.
Obs.: As estruturas SEdge e SVertex são auxiliares e são necessárias para destaque de vértices e arestas na interface do GRAFO.
| Nome | Tipo | Descrição |
|---|---|---|
u |
SVertex |
Vértice U - typedef int |
v |
SVertex |
Vértice V - typedef int |
(tabela 4.4)
Functions - Funções para manipulação de um grafo
A tabela 4.5 traz a lista de funções para manipulação do grafo. Com elas pode-se alocar e liberar memória para um grafo, inicializar as estruturas internas, copiar um grafo em outro, adicionar e remover vértices, arestas e arcos. E também limpar o status de marcado (mark) de vértices e arestas.
Obs.: Funções internas de controle não estão documentadas. A princípio elas não são necessárias para a construção de plugins.
| Declaração | Descrição |
|---|---|
void AllocGraph(Graph *G) |
Aloca espaço para um grafo e as estruturas que o compõem (vértices, arestas, matriz de adjacência, etc) |
void FreeGraph(Graph *G) |
Libera espaço alocado para grafo e suas estruturas |
void InitGraph(Graph *G, GraphType type) |
Inicializa um grafo e suas estruturas |
void InitEdges(Graph *G) |
Inicializa somente a matriz de adjacência e suas propriedades |
void CopyGraph(Graph *H, Graph *G) |
Aloca o grafo H e copia o G nele |
void AddPoint(Graph *G, float x, float y) |
Adiciona a vértice na posição (x,y) |
void RemovePoint(Graph *G, int p) |
Remove o vértice o P vértice do grafo |
void AddEdge(Graph *G, int x, int y) |
Adiciona um aresta entre os vértices X e Y |
void RemoveEdge(Graph *G, int x, int y) |
Remove a aresta entre os vértices X e Y |
void AddArc(Graph *G, int x, int y) |
Adciona o arco entre os vértice X para Y |
void RemoveArc(Graph *G, int x, int y) |
Remove a aresta direcionada do vértice X para Y |
void ClearMarkedVerts(Graph *G) |
Limpa a propriedade mark dos vértices |
void ClearMarkedEdges(Graph *G) |
Limpa a propriedade mark das arestas |
(tabela 4.5)
pgin.h
No header pgin.h estão declarados a estrutura para a lista de algoritmos bem como funções para entrada de parâmetros.
Pgin struct - Estrutura da lista de funções
A estrutura Pgin é uma lista de funções (algoritmos) disponíveis em um plugin.
Cada plugin deve possuir no mínimo uma função sempre terminada pelo tipo PGIN_LIST_END
ao final do capítulo 4 a criação de plugins de exemplo irão abordar a correta construção
da lista de algoritmos disponíveis em um plugin. A tabela 4.6 detalha os campos
da estrutura. São eles: Tipo do algoritmo, nome para o menu, nome da função
principal do algoritmo e flags de controle para o GRAFO.
| Nome | Tipo | Descrição |
|---|---|---|
type |
int |
Determina o tipo do plugin na lista de algoritmos |
label |
char * |
Determina o nome do algoritmo. Este é nome que irá aparecer na entrada do menu Algorithms |
name |
char * |
Determina o nome da função do algoritmo dentro do plugin |
flags |
int |
Passa informações ao GRAFO de como tratar esse algoritmo após a sua execução |
(tabela 4.6)
A tabela 4.7 detalha o valor para o campo type na lista de algoritimos.
| Nome | Descrição |
|---|---|
PGIN_TEST_ALG |
Informa que o algoritmo é de testes |
PGIN_RESULT_ALG |
Informa que o algoritmo é de resultado |
PGIN_STEP_ALG |
Informa que o algoritmo é de passo a passo |
PGIN_TRANSF_ALG |
Informa que o algoritmo é de transformação |
PGIN_SEARCH_ALG |
Informa que o algoritmo é de busca |
PGIN_LIST_END |
Final da lista de algoritmos |
(tabela 4.7)
O campo flag detalhado na tabela 4.8 informa ao GRAFO como ele deve redesenhar o grafo resultante ao
termino da execução de um algoritmo de transformação. Os demais tipos de plugins
não são sensíveis a estes flags e os grafos não serão redesenhados ao término da execução
destes plugin.
| Nome | Descrição |
|---|---|
PGIN_FLAG_NOREDRAW |
Não redesenha o grafo. O construtor do plugin é responsável por determinar a posição dos vértices |
PGIN_FLAG_REDRAWASCIRCLE |
Redesenha o grafo automaticamente em circulo |
PGIN_FLAG_REDRAWWITHCENTEREDVERTEX |
Redesenha o grafo com o primeiro vértice no centro |
(tabela 4.8)
Functions - Funções de entrada de dados a um plugin
A tabela 4.9 traz a lista de funções para manipulação de entrada de dados para os plugins. Com elas é possível fazer a leitura dos tipos de dados: Inteiro, Double e String.
| Declaração | Descrição |
|---|---|
int pgin_read_int(char *name, char *label, |
Cria janela para leitura de um tipo de dado inteiro |
double pgin_read_double(char *name, char *label, |
Cria janela para leitura de um tipo de dado double |
char *pgin_read_string(char *name, char *label, |
Cria janela para leitura de uma tipo de dado string |
(tabela 4.9)
A tabela 4.10 detalha os parâmetros das funções de entrada de dados descritas na tabela 4.9.
| Parâmetros | Descrição |
|---|---|
name |
Nome da janela |
label |
Texto informativo |
def |
Valor padrão |
min |
Mínimo valor permitido |
max |
Máximo valor permitido |
inc |
Incremento para int e double |
digits |
Número de casas decimais |
max_len |
Tamanho máximo da string |
(tabela 4.10)
alghandler.h
No header alghandler.h estão declarados as estruturas das listas de algoritmos bem como as funções utilizadas para manipula-las.
A tabela 4.11 detalha a função RunAlgorithm que pode ser utilizada para chamar qualquer algoritmo existente no grafo sendo ele nativo ou não. As listas especiais de destaque arc_edges e verts serão abordadas neste capítulo no tópico Estrutura de um plugin.
| Declaração | Descrição |
|---|---|
int RunAlgorithm(char *name, Graph *G, char *s, |
Chama qualquer algoritmo disponível sendo ele nativo ou por plugins |
(tabela 4.11)
list.h
No header list.h estão declarados as estruturas de pilha e lista. Bem como as funções utilizadas para manipula-las. Elas são necessárias no destaque de vértices e arestas. Vide o tópico Destacando vértices e arestas neste capítulo.
Node struct - Estrutura de um nodo
A estrutura Node na tabela 4.12 contém um nodo genérico onde o campo data pode apontar
para qualquer tipo de dado. O nodo pode ser utilizado tanto em uma lista ou em uma pilha.
| Nome | Tipo | Descrição |
|---|---|---|
data |
void * |
Aponta para o dado do Node |
size |
int |
Tamanho alocado para o dado apontado |
next |
Node * |
Aponta para o próximo nodo |
prev |
Node * |
Aponta para o nodo anterior |
(tabela 4.12)
Functions - Funções para manipulação de um nodo
A tabela 4.13 traz a lista de funções para criação e destruição de um nodo.
| Declaração | Descrição |
|---|---|
Node MakeNode(void *data, int size) |
Cria um nodo apontando para um dado informado com o tamanho de size |
void DestroyNode(Node n) |
Destrói o nodo informado |
(tabela 4.13)
List struct - Estrutura de uma lista
A estrutura List (tabela 4.14) contém os dados necessários para se trabalhar com o tipo de dado lista.
| Nome | Tipo | Descrição |
|---|---|---|
size |
int |
Número de nodes |
head |
Node |
Primeiro node |
tail |
Node |
Último node |
(tabela 4.14)
Functions - Funções para manipulação de uma lista
A tabela 4.15 contém a lista de funções para manipulação da estrutura list podendo-se com elas: Criar e inicializar uma lista, inserir e remover um nodo, mover, copiar e limpar uma lista.
| Declaração | Descrição |
|---|---|
List *CreateList(void) |
Cria uma lista |
void InitList(List *list) |
Inicializa a lista informada |
void InsertNode(List *list, Node node) |
Insere um nodo na lista informada |
Node RemoveNode(List *list, Node node) |
Remove o nodo na lista informada |
void MoveList(List *l1, List *l2) |
Copia a L2 em L1 destruindo L2; L1 deve estar inicializada |
void CleanList(List *list) |
Remove todos os nodos de uma lista |
void CopyList(List *l1, List *l2) |
Copia a L2 em L1; L1 deve estar inicializada |
(tabela 4.15)
Stack struct - Estrutura de uma pilha
A estrutura Stack (tabela 4.16) contém os dados necessários para se trabalhar com o tipo de dado pilha no GRAFO.
| Nome | Tipo | Descrição |
|---|---|---|
size |
int |
Número de nodes |
top |
Node |
Topo da pilha |
(tabela 4.16)
Functions - Funções para manipulação de uma pilha
A tabela 4.17 contém a lista de funções para manipulação da estrutura Stack podendo-se com elas: Criar e inicializar uma pilha, inserir e remover um nodo e limpar a pilha.
| Declaração | Descrição |
|---|---|
Stack *CreateStack(void) |
Cria uma pilha |
void InitStack(Stack *stk) |
Inicializa a pilha informada |
void PushNode(Stack *stk, Node node) |
Insere o nodo na pilha |
Node PopNode(Stack *stk) |
Remove o nodo da pilha |
void CleanStack(Stack *stk) |
Remove todos os nodos da pilha |
(tabela 4.17)
Neste tópico será abortado a criação do plugin Hello World e também o detalhamento da estrutura e divisões de um plugin. O código fonte completo do plugin Hello Word encontra-se no Apêndice B.
O plugin é dividido em 3 partes básicas. São elas:
Na primeira parde deve-se incluir os headers da linguagem C e os headers obrigatórios para os plugins:
27 28 29 30 31 32 33 34 35 36 | /* headers da linguagem C */
#include <stdio.h>
#include <stdlib.h>
/* headers do GRAFO */
/* Informacoes da estrutura de plugins */
#include "../pgin.h"
/* Informacoes da estrutura do GRAFO */
#include "../graph.h"
|
Obs.: Os headers do grafo foram incluídos pressupondo que a diretório plugins está um nível abaixo do diretório do GRAFO.
Na segunda parte deve-se declarar o protótipo para a função obrigatória pgin_info o protótipo para as funções de algoritmos e outras funções internas ao plugin. Como função de algoritmo foi declarado o tradicional HelloWorld.
38 39 40 41 42 43 44 45 46 | /* Funcao obrigatoria pgin_info */
Pgin *pgin_info(void);
/* Funcoes de algoritmos */
int HelloWorld(Graph *G, char *mess);
/* Funcoes internas ao plugin*/
...
...
|
As funções de algoritmos possuem uma assinatura diferente para a lista de parâmetros de acordo com o seu tipo. Essa diferença deve ser observada ao incluir o algoritmo na lista de funções do plugin.
int TestAlgorithm(Graph *G, char *mess)
int ResultAlgorithm(Graph *G, char *mess, List *arc_edges, List *verts)
int StepAlgorithm(Graph *G, char *mess, int indx, List *arc_edges, List *verts)
int Transformation(Graph *G, char *mess)
int SearchAlgorithm(Graph *G, char *mess, int indx, List *arc_edges, List *verts)A tabela 4.18 traz o detalhamento dos parâmetros passados as funções de algoritmos.
| Parâmetros | Descrição |
|---|---|
Graph *G |
Aponta para grafo na área de trabalho |
char *mess |
Aponta para a mensagem na barra de status |
int indx |
Número do vértice inicial de buscas |
List *arc_edges |
Lista com as arestas destacadas do grafo na área de trabalho |
List *verts |
Lista com os vértices destacados do grafo na área de trabalho |
(tabela 4.18)
É importante destacar que o grafo G passado como parâmetro aponta para a estrutura do grafo que será desenhada na área de trabalho. E as listas arc_edges e verts apontam para as estruturas de destaque de vértices e arestas. Ao iniciar o GRAFO estas estruturas são alocadas e disponibilizadas para utilização. Um plugin pode reinicializa-las com InitGraph, InitEdges e CleanList. Porem NÃO deve liberar a memória alocadas a elas.
Na terceira parte deve-se criar o corpo para a função obrigatória pgin_info e implementar as funções do algoritmo.
pgin_info - Função obrigatória
A pgin_info é responsável por inicializar a lista de funções existentes no plugin. No exemplo abaixo incluímos a função HelloWorld do tipo PGIN_TEST_ALG.
47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 | /* A funcao pgin_info() deve sempre estar presente. O GRAFO ira chama-la
* para recuperar as informacoes do plugin.
*/
Pgin *pgin_info(void){
Pgin *pgin;
/* Aloca espaco para o HelloWorld e o PGIN_LIST_END */
pgin = (Pgin *) malloc(2 * sizeof(Pgin));
/* Inclui HelloWorld como primeiro algoritmo do plugin */
pgin[0].type = PGIN_TEST_ALG;
pgin[0].label = "Hello World!";
pgin[0].name = "HelloWorld";
pgin[0].flags = 0;
/* Indica o final da lista de algoritmos */
pgin[1].type = PGIN_LIST_END;
pgin[1].label = 0;
pgin[1].name = 0;
pgin[1].flags = 0;
return pgin;
}
|
Como já foi dito um plugin pode conter vários algoritmos, para isso basta incluí-los na lista. Por exemplo se o algoritmo HelloUniverse estivesse no mesmo plugin que o HelloWorld a função pgin_info deveria ser:
47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 | /* A funcao pgin_info() deve sempre estar presente. O GRAFO ira chama-la
* para recuperar as informacoes do plugin.
*/
Pgin *pgin_info(void){
Pgin *pgin;
/* Aloca espaco para o HelloWorld, HelloUniverse e o PGIN_LIST_END */
/* Observe que agora o malloc aloca um espaco a mais para o HelloUniverse */
pgin = (Pgin *) malloc(3 * sizeof(Pgin));
/* Inclui HelloWorld como primeiro algoritimo do plugin */
pgin[0].type = PGIN_TEST_ALG;
pgin[0].label = "Hello World!";
pgin[0].name = "HelloWorld";
pgin[0].flags = 0;
/* Inclui HelloUniverse como primeiro algoritmo do plugin */
pgin[1].type = PGIN_TEST_ALG;
pgin[1].label = "Hello Universe!!!";
pgin[1].name = "HelloUniverse";
pgin[1].flags = 0;
/* Indica o final da lista de algoritmos */
pgin[2].type = PGIN_LIST_END;
pgin[2].label = 0;
pgin[2].name = 0;
pgin[2].flags = 0;
return pgin;
}
|
HelloWorld - Funções de algoritmos
E finalmente a implementação da função de algoritmo. Quando o nosso exemplo for executado será escrito na barra de status Hello World!.
71 72 73 74 75 76 77 | /* Esta e a funcao principal do plugin */
int HelloWorld(Graph *G, char *mess){
sprintf(mess, "Hello World!");
return 1;
}
|
Para que o plugin seja reconhecido pelo GRAFO devemos criar uma biblioteca dinâmica e inclui-lo no diretório destinado aos plugins.
gcc -Wall -fPIC -shared hw.c -o hw.so
Ao abrir o GRAFO os plugins serão carregados e um item de menu criado para cada função neles contidas. No nosso exemplo o plugin HelloWorld criou a entrada de menu abaixo. Figura 4.1:
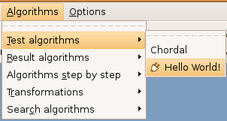
(figura 4.1)
Ao clicar no menu Hello World! o GRAFO chama a função de algoritmo associado a ele. E ao termino atualiza a área de trabalho e a barra de status com os resultados. No nosso exemplo simplesmente escreve na barra de status. Figura 4.2.

(figura 4.2)
Neste tópico será abordado a criação do plugin Get some parameters que ilustra a utilização das funções de entrada de dados para o GRAFO. O código fonte completo do plugin Get some parameters encontra-se no Apêndice B.
Os plugins podem receber 3 tipos de dados.
54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 | int getsp(Graph *G, char *mess){
int i;
double d;
char *s;
i = pgin_read_int("Get some parameters", "Give me an int",
10, 1, 2000000, 1);
d = pgin_read_double("Get some parameters", "Give me a double",
0.0, -10.0, 10.0, 0.1, 1);
s = pgin_read_string("Get some parameters", "Give me a string",
"I'm a string", 40);
sprintf(mess, "I got: %d, %f and '%s'. Thanks!", i, d, s);
free(s);
return 1;
}
|
Como resultado obtemos os seguintes diálogos de entrada de dados. Para um inteiro figura 4.3. Para um double figura 4.4. Para uma string figura 4.5.
 |
 |
 |
| (figura 4.3) | (figura 4.4) | (figura 4.5) |
E os valores recebidos pelos diálogos são escritos na barra de status. Vide figura 4.6

(figura 4.6)
Neste tópico será abordado a criação do plugin Generate Star Graph que ilustra a utilização das funções AddPoint e AddEdge detalhadas na tabela 4.5. Abaixo segue a função principal no arquivo stargraphexample.c. O código fonte completo do plugin Generate Star Graph encontra-se no Apêndice B.
59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 | int stargraph(Graph *G, char *mess){
int i, n;
/* Le o numero de vertices do grafo */
n = pgin_read_int("Generate Star Graph", "Number of vertices",
5, 1, 2000000, 1);
/* Inicializar o grafo da area de trabalho */
InitGraph(G, G->type);
/* Adiciona N vertices na posicao (0,0) */
for (i = 0; i < n; i++)
AddPoint(G, 0, 0);
/* Adiciona N arestas comecando no vertice 0 ate N-1 */
for (i = 1; i < n; i++) {
AddEdge(G, 0, i);
}
return 1;
}
|
Como pode ser observado o algoritmo não se preocupa em posicionar de maneira elegante os vértices na tela. Adicionando todos os vértices sempre na posição (0,0).
67 68 69 70 71 72 73 | ...
/* Adiciona N vertices na posicao (0,0) */
for (i = 0; i < n; i++)
AddPoint(G, 0, 0);
...
|
Isto é possível porque o plugin de transformação criado está utilizando o flag PGIN_FLAG_REDRAWWITHCENTEREDVERTEX. E com isso o grafo gerado será redesenhado automaticamente com o primeiro vértice no centro. Se estivéssemos utilizando o flag PGIN_FLAG_NOREDRAW o plugin deve responsável por posicionar os vértices corretamente na área de trabalho.
Como resultado a geração de um grafo estrela com 20 vértices. Figura 4.7:
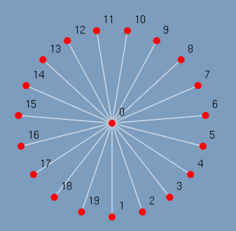
(figura 4.7)
Neste tópico será abordado a construção do plugin Highest Degree que ilustra a utilização da lista especial verts e a construção do plugin Some Edge que ilustra a utilização da lista especial arc_edges. O destaque de vértices e arestas utilizam as listas especiais passadas como parâmetros aos plugins. A lista verts contém os vértices destacados em um grafo. A lista arc_edges contém as arestas e arcos destacados em um {di,}grafo. Para o destaque deve-se simplesmente inserir um nodo nas listas a ao encerrar a execução do algoritmo o GRAFO se encarrega de destacar na interface os nodos inseridos. O detalhamento sobre as funções para manipulação de nodos e listas estão respectivamente nas tabelas 4.13 e 4.15.
Abaixo segue a função principal no arquivo vertexexample.c responsável pelo plugin Highest Degree que ilustra a utilização da lista especial verts. O código fonte completo do plugin Highest Degree encontra-se no Apêndice B.
94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 | int MaxDegree(Graph *G, char *mess, List *arc_edges, List *verts){
Node N;
int i,maxdeg;
/* Testa se o grafo esta vazio */
if (G->size < 1) {
sprintf(mess, "%s", "Empty graph!");
return 1;
}
/* Procurar pelo vertice de maior grau */
maxdeg = 0;
for (i = 1; i < G->size; i++) {
if (G->vertex[i].degree > G->vertex[maxdeg].degree) {
maxdeg = i;
}
}
/* Coloca em um novo nodo o vertice de maior grau */
N = MakeNode(&maxdeg, sizeof(int));
/* Coloca o nodo na lista de vertices especiais */
InsertNode(verts, N);
return 1;
}
|
Utiliza-se da função MakeNode para criar um novo nodo e depois da função InsertNode para inserir um nodo com o vértice de maior grau na lista verts.
Como resultado o destaque do vértice 1 de grau 5 no grafo abaixo. Figura 4.8:
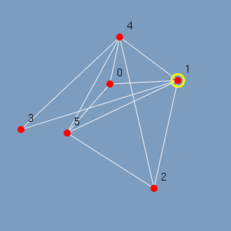
(figura 4.8)
Abaixo segue a função principal no arquivo edgeexample.c responsável pelo plugin Some Edge que ilustra a utilização da lista especial arc_edges. O código fonte completo do plugin Some Edge encontra-se no Apêndice B.
96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 | int MaxMinEdge(Graph *G, char *mess, List *arc_edges, List *verts){
SEdge E; /* Aresta simples */
Node N;
int i,maxdeg,mindeg;
/* Testa se o grafo esta vazio */
if (G->size < 1) {
sprintf(mess, "%s", "Empty graph!");
return 1;
}
/* Procurar pelo vertice de maior grau */
maxdeg = 0;
for (i = 1; i < G->size; i++) {
if (G->vertex[i].degree > G->vertex[maxdeg].degree) {
maxdeg = i;
}
}
/* Procura pelo vertice de menor grau adjacente ao de maior */
mindeg = -1;
for (i = 0; i < G->size; i++) {
if (G->edge[maxdeg][i]) {
if (mindeg == -1) {
mindeg = i;
} else if (G->vertex[i].degree < G->vertex[mindeg].degree) {
mindeg = i;
}
}
}
/* Atribui maxdeg e o mindeg a aresta simples */
E.u = maxdeg;
E.v = mindeg;
/* Coloca em um novo nodo a aresta simples */
N = MakeNode(&E, sizeof(SEdge));
/* Coloca o nodo na lista de arestas especiais */
InsertNode(arc_edges, N);
return 1;
}
|
Como no exemplo do vértice também se utiliza a função MakeNode para criar um novo nodo. Porem o nodo criado contém como dado uma aresta simples (SEdge). E depois utiliza-se da função InsertNode para inserir o nodo com a aresta encontrada na lista arc_edges.
Como resultado o destaque da aresta entre o vértice 1 de grau 5 e o vértice 3 de grau 2. Figura 4.9:
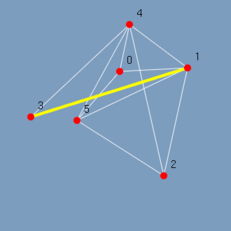
(figura 4.9)
Neste capítulo, inicialmente, é feito um comparativo entre a execução de um algoritmo normal; recurso já existente no GRAFO; e a execução de um algoritmo passo a passo, novo recurso introduzido por este trabalho. também são explicados os recursos existentes no passo a passo e como o usuário pode interagir com um algoritmo. Em seguida é abordado como o este foi implementado e o que motivou esta abordagem. O capítulo termina mostrando um tutorial prático de como se realiza a implementação um plugin com funcionalidade passo a passo. Para tanto abordou-se neste tema também os headers necessários, as estruturas internas e os cuidados que devem ser tomados para sua construção.
O que é o passo a passo? É a possibilidade de interagir com a execução do algoritmo. E com isso conseguir uma visão melhor de como e o que ele faz do seu início ao fim.
A possibilidade de execução de algoritmos passo a passo veio preencher uma lacuna deixada pelo GRAFO. Na estrutura de execução que existia até então era difícil observar o que se passava entre o início (click no menu) e o fim do algoritmo (atualização da área de trabalho).
Observemos a execução do algoritmo Depth First - Busca em profundidade, sem suporte a passo a passo, no menu Algorithms > Search algorithms > Depth First.
Na figura (5.1) observa-se um grafo em árvore com 6 vértices. Ao executar o algoritmo em segundos todos os vértices e arestas da árvore são destacados. Vide figura (5.2). Como a árvore foi completamente destacada? Qual a ordem que os vértices foram destacados? Quantos passos têm esse algoritmo? Sem o conhecimento prévio de como funciona a busca em profundidade em uma árvore é impossível responder a tais perguntas.
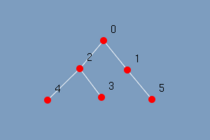 |
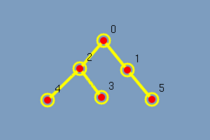 |
| (figura 5.1) | (figura 5.2) |
Foi justamente com o objetivo de responder a estas perguntas que entra a execução de algoritmo passo a passo na interface do GRAFO. Ele vem auxiliar a compreensão e o entendimento da execução de algoritmos de uma maneira visual e interativa.
Observemos a execução do mesmo algoritmo Depth First - Busca em profundidade, porém com suporte a passo a passo, no menu Algorithms > Algorithms step by step > Depth First.
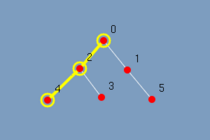
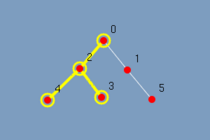
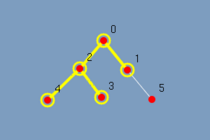
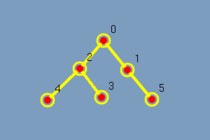
Na figura 5.3 observa-se o mesmo grafo em árvore com 6 vértices. Ao executar o algoritmo o grafo vai lentamente sendo destacado. Vide figura 5.4 até figura 5.9. Com esta visualização mesmo um leitor leigo consegue responder as perguntas feitas.
Como a árvore foi completamente destacada?
Qual a ordem que os vértices foram destacados?
Quantos passos tem esse algoritmo?
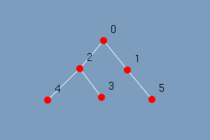 |
||
| (figura 5.3) | ||
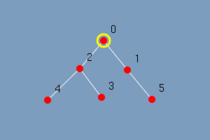 |
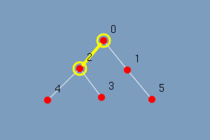 |
 |
| (figura 5.4) | (figura 5.5) | (figura 5.6 |
 |
 |
 |
| (figura 5.7) | (figura 5.8) | (figura 5.9) |
Através da barra de ferramentas, figura 5.10, é possível uma interação básica com o algoritmo. Ao acionar o algoritmo pelo menu ele lentamente vai sendo executado, porem é possível através dos botões ir direto ao resultado final, voltar ao começo, ir somente um passo a diante, retroceder um passo ou colocá-lo para executar passo a passo novamente.

(figura 5.10)
A idéia inicial foi implementar a interface passo a passo de uma forma genérica sem que fosse necessária intervenção explícitas nos algoritmo. E assim todo e qualquer algoritmo no GRAFO poderia ser executado com ou sem o passo a passo, porem devido a modularidade do programa fez com que essa abordagem não fosse possível. No GRAFO existe uma clara divisão entre o que é interface com o usuário, estrutura de desenho, estrutura de grafos e estrutura de plugins e algoritmos. Os algoritmos nativos ou por plugins não têm acesso direto a interface com o usuário e a estrutura de desenho. Ao serem executados eles se preocupam em manipular grafos, arestas e vértices. O reflexo desta alterações ao usuário é feito pela estrutura de desenho em conjunto com a interface.
A estratégia adotada foi de que os algoritmos continuassem a manipular somente o que eles conhecem, que são grafos, arestas e vértices, para isto, foi criado um mecanismo de gravação e reprodução de estados. A cada estado interessante o algoritmo explicitamente grava a situação do grafo e das listas de destaque de vértices e arestas. Ao concluir a execução temos um filme com os passos relevantes para a compreensão do algoritmo. E este filme é disponibilizado ao usuário.
Para criar o mecanismo de gravação e reprodução utilizou-se uma lista onde cada nodo contém em que contexto está o grafo, arestas e vértices em destaque no momento que se instrui a gravação. Abaixo segue as estruturas e funções implementadas para tratar o passo a passo.
step.h
O header step.h deve ser incluído em um plugin sempre que se desejar que este tenha os recursos do passo a passo
Step struct - Estrutura de um passo
A estrutura Step (tabela 5.1) contém as informações necessárias a um passos que são: O seu identificador, uma cópia do grafo, os vértices em destaque, as arestas em destaque e uma mensagem associada ao passo salvo.
| Nome | Tipo | Descrição |
|---|---|---|
id |
int |
Identificador do passo. Auto incremental e único |
G |
Graph |
Grafo associado ao passo |
SpecEdges |
List * |
Lista de destaque de arestas associadas ao passo |
SpecVerts |
List * |
Lista de destaque de vértices associados ao passo |
status_string |
char[1000] |
Mensagem para a barra de status associada ao passo |
(tabela 5.1)
StepStruct struct - Estrutura de múltiplos passos
A estrutura StepStruct (tabela 5.2) contém as informações necessárias para a reprodução dos passo: A quantidade de passos salvos, o passo atual, a lista de passos salvos e o status da execução do passo a passo.
| Nome | Tipo | Descrição |
|---|---|---|
size |
int |
Número de passos gravados |
index |
int |
Contador de passo. Informa o passo atual |
steps |
Step[MAX_STEPS] |
Lista contendo os passos gravados |
exec_state |
char |
Status de execução (EXECUTING_STEPS, NOT_EXECUTING_STEPS) |
(tabela 5.2)
Functions - Funções para manipulação do passo a passo
A tabela 5.3 traz a lista de funções para manipulação do passo a passo. A função AddStep é a única de uso externo, através de plugins, as demais são de uso interno a implementação do passo a passo. Um algoritmo somente deve-se preocupar em salvar os passos através do AddStep a inicialização da estrutura Step e StepStruct e o início automático da execução são atribuições da interface do GRAFO.
| Declaração | Descrição |
|---|---|
void InitStepStruct(void) |
Inicializa a estrutura passo a passo |
void AddStep(Graph *G, List *arc_edges, List *verts) |
Adiciona o grafo G e as listas arc_edges e verts no próximo passo livre |
void ShowStep(Graph *G, List *arc_edges, List *verts, int step) |
Vai para o passo informado e o copia para a interface o grafo G e as listas arc_edges e verts |
void FirstStep(Graph *G, List *arc_edges, List *verts) |
Vai para o primeiro passo gravado e o copia para a interface o grafo G e as listas arc_edges e verts |
void PreviousStep(Graph *G, List *arc_edges, List *verts) |
Vai para o passo anterior e o copia para a interface o grafo G e as listas arc_edges e verts |
void NextStep(Graph *G, List *arc_edges, List *verts) |
Vai para o próximo passo e o copia para a interface o grafo G e as listas arc_edges e verts |
void LastStep(Graph *G, List *arc_edges, List *verts) |
Vai para o último passo e o copia para a interface o grafo G e as listas arc_edges e verts |
int GetLastStep(void) |
Retorna o número de passos gravados |
char GetExecStateStep(void) |
Retorna se o passo a passo está em execução (EXECUTING_STEPS, NOT_EXECUTING_STEPS) |
void SetExecStateStep(char state) |
Inicia e termina a execução do passo a passo (START_EXEC_STEPS, STOP_EXEC_STEPS) |
(tabela 5.3)
Como exemplo prático será construído o plugin Select odd que tem como característica destacar todos os vértices ímpares e todas as arestas que conectam vértices ímpares. O código fonte completo do plugin Select odd encontra-se no Apêndice B.
No capítulo 4 foi abordada a construção de plugins. Neste capítulo iremos complementá-la com a possibilidade de plugins passo a passo. Como no plugin comum o passo a passo também é dividido em 3 partes. São elas:
Na primeira parte deve-se incluir os headers da linguagem C e os headers obrigatórios para todos os plugins e mais o header step.h obrigatório para o passo a passo:
31 32 33 34 35 36 37 38 39 40 41 42 43 | /* headers da linguagem C */
#include <stdio.h>
#include <stdlib.h>
/* headers do GRAFO */
/* Informacoes da estrutura de plugins */
#include "../pgin.h"
/* Informacoes da estrutura do GRAFO */
#include "../graph.h"
/* Informacoes da estrutura do Passo a Passo */
#include "../step.h"
|
Na segunda parte declara-se o protótipo para a função obrigatória pgin_info e o protótipo para as funções de algoritmos e outras funções. Como função de algoritmo foi declarada a SelectOdd.
45 46 47 48 49 50 51 52 53 | /* Funcao obrigatoria pgin_info */
Pgin *pgin_info(void);
/* Funcoes de algoritmos */
int SelectOdd(Graph *G, char *mess, int indx, List *arc_edges, List *verts);
/* Funcoes internas ao plugin*/
...
...
|
Como mencionado no capítulo 4 cada tipo de algoritmo possui uma assinatura diferente para a lista de parâmetros (tabela 5.4). Para algoritmos passo a passo temos:
int StepAlgorithm(Graph *G, char *mess, int indx, List *arc_edges, List *verts)
| Parâmetros | Descrição |
|---|---|
Graph *G |
Aponta para grafo na área de trabalho |
char *mess |
Aponta para a mensagem na barra de status |
int indx |
Número do vértice inicial de buscas |
List *arc_edges |
Lista com as arestas destacadas do grafo na área de trabalho |
List *verts |
Lista com os vértices destacados do grafo na área de trabalho |
(tabela 5.4)
Análogo a algoritmos tradicionais a terceira parte deve-se criar o corpo para a função obrigatória pgin_info e implementar as funções do algoritmo.
pgin_info - Função obrigatória
A pgin_info deve adicionar a lista de algoritmos com o tipo correto para algoritmos passo a passo que é PGIN_STEP_ALG.
54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 | /* A funcao pgin_info() deve sempre estar presente. O GRAFO ira chama-la
* para recuperar as informacoes do plugin.
*/
Pgin *pgin_info(void){
Pgin *pgin;
/* Aloca espaco para o SelectOdd e o PGIN_LIST_END */
pgin = (Pgin *) malloc(2 * sizeof(Pgin));
/* Inclui SelectOdd como primeiro algoritmo do plugin */
pgin[0].type = PGIN_STEP_ALG;
pgin[0].label = "Select odd";
pgin[0].name = "SelectOdd";
pgin[0].flags = 0;
/* Indica o final da lista de algoritmos */
pgin[1].type = PGIN_LIST_END;
pgin[1].label = 0;
pgin[1].name = 0;
pgin[1].flags = 0;
return pgin;
}
|
SelectOdd - Funções de algoritmos
A função SelectOdd deve-se preocupar em gravar passos que ilustram a execução do algoritmo, os passos gravados que serão disponibilizado para a interação do usuário.
79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 | int SelectOdd(Graph *G, char *mess, int indx, List *arc_edges, List *verts) {
SEdge E; /* Single Edge */
Node N;
int i, j,oddvertex;
/* Testa se o grafo e vazio */
if (G->size < 1) {
sprintf(mess, "%s", "Empty graph!");
return 1;
}
/* Seta para falso (0) a propriede 'mark' em todos os vertices */
ClearMarkedVerts(G);
/* Adiciona o primeiro passo - Nada destacado */
AddStep(G, arc_edges, verts);
/* Procura e destaca os vertices impares */
oddvertex = 0;
for (i = 1; i < G->size; i++) {
/* Verifica se i e um numero impar */
if ((i % 2)) {
/* Marca o vertices para uso futuro */
G->vertex[i].mark = 1;
oddvertex = i;
/* Coloca em um novo nodo o vertice impar */
N = MakeNode(&oddvertex, sizeof(int));
/* Coloca o nodo na lista de vertices especiais */
InsertNode(verts, N);
/* Adiciona novo passo - Salva o vertice destacado */
AddStep(G, arc_edges, verts);
}
}
/* Seta para falso (0) a propriede 'mark' em todas as arestas */
ClearMarkedEdges(G);
/* Procura por um vertice impar adjacente a outro vertice impar */
for (i = 0; i < G->size; i++) {
for (j = 0; j < G->size; j++) {
/* Evita o salvamento do passo [j,i] porque o passo [i,j] ja foi salvo */
if (!G->prop[j][i].mark && \
/* Verdadeiro se o vertex[i] e adjacente ao vertex[j] */
G->edge[i][j] && \
/* Verdadeiro se o vertex[i] e um vertice impar */
G->vertex[i].mark && \
/* Verdadeiro se o vertex[j] e um vertice impar */
G->vertex[j].mark) {
/* Marca a aresta para uso futuro */
G->prop[i][j].mark = 1;
/* Atribui um vertice impar adjacente a outro vertice impar no vertice simples */
E.u = i;
E.v = j;
/* Coloca em um novo nodo a aresta simples */
N = MakeNode(&E, sizeof(SEdge));
/* Coloca o nodo na lista de arestas especiais */
InsertNode(arc_edges, N);
/* Adiciona novo passo - Salva a aresta destacada */
AddStep(G, arc_edges, verts);
}
}
}
return 1;
}
|
No algoritmo Select odd foi utilizado três vezes a chamada da função AddStep. A primeira vez se preocupa em salvar contexto do grafo sem o destaque de vértices e arestas. A segunda chamada se preocupa em salvar o momento que vértices ímpares são inseridos na lista especial verts. A terceira chamada se preocupa em salvar o momento em que as arestas são inseridas na lista especial arc_edges. A segunda chamada da função AddStep poderia ser suprimida. E com isso os vértices e arestas apareceriam em destaque no passo a passo em conjunto. Com isso concluímos que o posicionamento da chamada AddStep no algoritmo é essencial para sua compreensão. No exemplo o que se deseja é mostrar que primeiramente todos os vértices impares são destacados e depois que todas as arestas entre vértices ímpares são destacadas.
Um outro cuidado que se deve ter é de não salvar passos adicionais ou repetidos que não acrescentem em nada a compreensão do algoritmo. No exemplo utiliza-se a propriedade mark para informar que uma aresta já foi destacada. Por exemplo se foi salvo o passo quando a aresta (1,3) é destacada não existe a necessidade de salvar o passo (3,1) pois a aresta é a mesma. Abaixo segue o trecho de código que faz este controle.
118 119 120 121 122 123 | ...
...
/* Evita o salvamento do passo [j,i] porque o passo [i,j] ja foi salvo */
if (!G->prop[j][i].mark && \
...
|
128 129 130 131 132 133 134 | ...
/* Marca a aresta para uso futuro */
G->prop[i][j].mark = 1;
...
...
|
O procedimento de compilação deve ser reproduzido para os plugins passo a passo.
gcc -Wall -fPIC -shared selectoddexample.c -o selectoddexample.so
Ao abrir o GRAFO o novo plugin estará disposto abaixo do menu Algorithms > Algorithms step by step vide figura 5.11.
(figura 5.11)
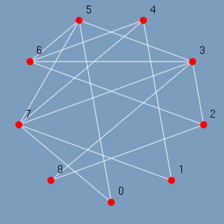
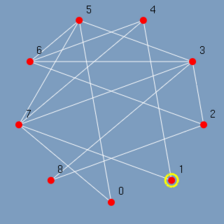
Ao clicar no menu Select odd o GRAFO chama a função de algoritmo associado a ele, o algoritmo é executado gravando todos os passos relevantes, e ao término o GRAFO exibe lentamente o resultado (Figura 5.12 até 5.20). Observando-se os passos pode-se ter uma idéia de como o algoritmo Select odd foi construído. Primeiro são destacados todos os vértices ímpares do menor para o maior {1, 3, 5, 7}. E depois todas as arestas entre vértices ímpares do menor vértice para o maior {(1,7), (3,5), (3,7), (5,7)}.
 |
 |
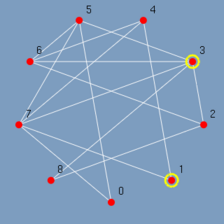 |
| (figura 5.12) | (figura 5.13) | (figura 5.14) |
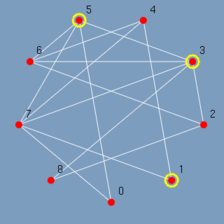 |
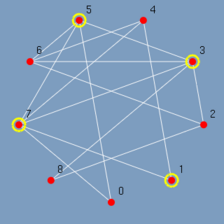 |
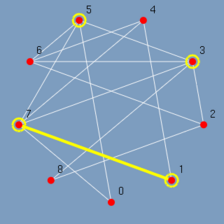 |
| (figura 5.15) | (figura 5.16) | (figura 5.17) |
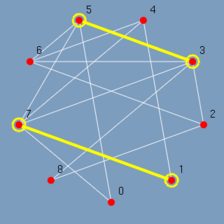 |
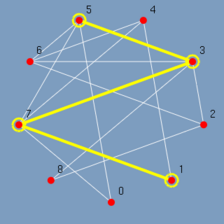 |
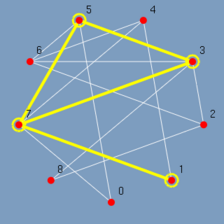 |
| (figura 5.18) | (figura 5.19) | (figura 5.20) |
A evolução de um software é um processo contínuo que envolve manutenções corretivas, implementação de novas funcionalidades e documentação. Este capítulo detalha o que foi realizado por este trabalho e expõem algumas idéias na intenção de convidar ao leitor a novas possibilidades de implementações e/ou manutenções no GRAFO.
Durante a confecção deste trabalho foram realizadas algumas manutenções corretivas e a implementação de novas funcionalidades como o passo a passo e este documento que serve como documentação para os trabalhos futuros. Tais implementações serão citadas uma a uma nos itens 6.1.1, 6.1.2 e 6.1.3 para que o leitor possa acompanhar e perceber a dimensão deste trabalho.
Além do que já foi realizado por este trabalho, foram observados outros pontos onde existe a possibilidade de manutenção corretiva e oportunidades de melhorias.
O GRAFO é um software livre sobre a GPL versão 2. Porem ele está restrito ao ambiente da UFPR. Como um software livre qualquer um pode contribuir para o seu desenvolvimento. Encontrar um repositório público e disponibiliza-lo para a comunidade dará longevidade ao software. O Apêndice A detalha como é possível obter os fontes a partir do repositório na UFPR.
Com este trabalho conseguiu-se cumprir com algumas estapas do processo de evolução do GRAFO. Fazendo-se manutenções corretivas, implementando-se novas funcionalidades e melhorando a documentação. A expectativa é que agora outros venham a cumprir outras etapas no processo, como realizado por Murilo Vicente, Oliver Matias e por mim.
Esse capitulo tem a intenção de auxiliar a quem vier a fazer uma futura manutenção ou melhoria no GRAFO. Mostra de maneira simplificada a estrutura de diretórios e o conteúdo de cada arquivo e os pacotes de dependência do GRAFO e onde pode-se obter os arquivos fontes.
Os fontes devem ser obtidos através do Subversion do AlgLab para isto deve-se solicitar a inclusão de sua chave pública ao professor André Guedes <andre@inf.upfr.br>.
ssh-keygen -t rsaEnviar o arquivo
{$HOME}\.ssh\id_rsa.pub ao professor André Guedes.
mkdir <DIRETÓRIO DO GRAFO> svn checkout svn+ssh://andre@fradim.inf.ufpr.br/alglab/grafo/ <DIRETÓRIO DO GRAFO>
Os pacotes abaixo relacionados são necessários para a compilação. Em muitos ambientes alguns destes já virão instalados por padrão. Esta lista foi obtida a partir de um Linux Ubuntu 7.10 com a sua instalação padrão.
cd <DIRETÓRIO DO GRAFO> cd src ./configure make
./grafo
/usr/bin. É necessário privilégio
de root para fazer esta operação.
make install
A seguir segue a estrutura de diretório e uma breve descrição do conteúdo dos arquivos que compõem o GRAFO.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 | /*
* grafo - graph editor
* Copyright (c) 2003
* Murilo Vicente Goncalves da Silva <murilo@pet.inf.ufpr.br>
* Oliver Matias van Kaick <oliver@pet.inf.ufpr.br>
* Ulisses Cordeiro Pereira <ulisses@cordeiropereira.com.br>
*
* This program is free software; you can redistribute it and/or modify
* it under the terms of the GNU General Public License as published by
* the Free Software Foundation; either version 2 of the License, or
* (at your option) any later version.
*
* This program is distributed in the hope that it will be useful,
* but WITHOUT ANY WARRANTY; without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
* See the GNU General Public License for more details (file COPYING).
*/
/* ******** */
/* * hw.c * */
/* ******** */
/* Plugin example: hello world */
/* C language headers */
#include <stdio.h>
#include <stdlib.h>
/* Here the GRAFO headers */
/* Add plugins information */
#include "../pgin.h"
/* Add graph struct information */
#include "../graph.h"
/* Mandatory function pgin_info */
Pgin *pgin_info(void);
/* algorithm function */
int HelloWorld(Graph *G, char *mess);
/* Others functions */
/* The pgin_info() function should always be present. GRAFO will call
* it to get the plugin information.
*/
Pgin *pgin_info(void){
Pgin *pgin;
/* Alocate space for HelloWorld and PGIN_LIST_END */
pgin = (Pgin *) malloc(2 * sizeof(Pgin));
/* Includes HelloWorld as the first algorithm of plugin */
pgin[0].type = PGIN_TEST_ALG;
pgin[0].label = "Hello World!";
pgin[0].name = "HelloWorld";
pgin[0].flags = 0;
/* It indicates the end of the list of algorithms */
pgin[1].type = PGIN_LIST_END;
pgin[1].label = 0;
pgin[1].name = 0;
pgin[1].flags = 0;
return pgin;
}
/* This is the plugin's main function */
int HelloWorld(Graph *G, char *mess){
sprintf(mess, "Hello World!");
return 1;
}
/* ******* */
/* * End * */
/* ******* */
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 | /*
* grafo - graph editor
* Copyright (c) 2003
* Murilo Vicente Goncalves da Silva <murilo@pet.inf.ufpr.br>
* Oliver Matias van Kaick <oliver@pet.inf.ufpr.br>
*
* This program is free software; you can redistribute it and/or modify
* it under the terms of the GNU General Public License as published by
* the Free Software Foundation; either version 2 of the License, or
* (at your option) any later version.
*
* This program is distributed in the hope that it will be useful,
* but WITHOUT ANY WARRANTY; without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
* See the GNU General Public License for more details (file COPYING).
*/
/* *********** */
/* * getsp.c * */
/* *********** */
/* Plugin example: get some input parameters */
#include <stdio.h>
#include <stdlib.h>
/* Here the GRAFO headers */
#include "../pgin.h"
#include "../graph.h"
Pgin *pgin_info(void);
int getsp(Graph *G, char *mess);
Pgin *pgin_info(void){
Pgin *pgin;
pgin = (Pgin *) malloc(2 * sizeof(Pgin));
pgin[0].type = PGIN_TEST_ALG;
pgin[0].label = "Get some parameters";
pgin[0].name = "getsp";
pgin[1].type = PGIN_LIST_END;
pgin[1].label = 0;
pgin[1].name = 0;
return pgin;
}
int getsp(Graph *G, char *mess){
int i;
double d;
char *s;
i = pgin_read_int("Get some parameters", "Give me an int",
10, 1, 2000000, 1);
d = pgin_read_double("Get some parameters", "Give me a double",
0.0, -10.0, 10.0, 0.1, 1);
s = pgin_read_string("Get some parameters", "Give me a string",
"I'm a string", 40);
sprintf(mess, "I got: %d, %f and '%s'. Thanks!", i, d, s);
free(s);
return 1;
}
/* ******* */
/* * End * */
/* ******* */
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 | /*
* grafo - graph editor
* Copyright (c) 2003-2008
* Ulisses Cordeiro Pereira <ulisses@cordeiropereira.com.br>
*
* This program is free software; you can redistribute it and/or modify
* it under the terms of the GNU General Public License as published by
* the Free Software Foundation; either version 2 of the License, or
* (at your option) any later version.
*
* This program is distributed in the hope that it will be useful,
* but WITHOUT ANY WARRANTY; without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
* See the GNU General Public License for more details (file COPYING).
*/
/* ******************* */
/* * stargraphexample.c * */
/* ******************* */
/* Plugin example: Generate a strar graph */
#include <stdio.h>
#include <stdlib.h>
/* Here the GRAFO headers */
/* Add plugins information */
#include "../pgin.h"
/* Add graph struct information */
#include "../graph.h"
/* Prototype functions */
Pgin *pgin_info(void);
int stargraph(Graph *G, char *mess);
/* This function returns the plugin info */
Pgin *pgin_info(void){
Pgin *pgin;
pgin = (Pgin *) malloc(2 * sizeof(Pgin));
pgin[0].type = PGIN_TRANSF_ALG;
pgin[0].label = "Generate Star Graph";
pgin[0].name = "stargraph";
pgin[0].flags = PGIN_FLAG_REDRAWWITHCENTEREDVERTEX;
pgin[1].type = PGIN_LIST_END;
pgin[1].label = 0;
pgin[1].name = 0;
pgin[1].flags = 0;
return pgin;
}
/* This is the plugin's main function */
int stargraph(Graph *G, char *mess){
int i, n;
/* Get number of vertices */
n = pgin_read_int("Generate Star Graph", "Number of vertices",
5, 1, 2000000, 1);
/* Generate graph */
InitGraph(G, G->type);
/* Adds N vertices in the position (0,0) */
for (i = 0; i < n; i++)
AddPoint(G, 0, 0);
/* Adds N edges starting at the vertex 0 to N-1 */
for (i = 1; i < n; i++) {
AddEdge(G, 0, i);
}
return 1;
}
/* ******* */
/* * End * */
/* ******* */
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 | /*
* grafo - graph editor
* Copyright (c) 2003-2008
* Murilo Vicente Goncalves da Silva <murilo@pet.inf.ufpr.br>
* Oliver Matias van Kaick <oliver@pet.inf.ufpr.br>
* Ulisses Cordeiro Pereira <ulisses@cordeiropereira.com.brr>
*
* This program is free software; you can redistribute it and/or modify
* it under the terms of the GNU General Public License as published by
* the Free Software Foundation; either version 2 of the License, or
* (at your option) any later version.
*
* This program is distributed in the hope that it will be useful,
* but WITHOUT ANY WARRANTY; without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
* See the GNU General Public License for more details (file COPYING).
*/
/* ******************* */
/* * vertexexample.c * */
/* ******************* */
/* Plugin example: This program does not compute anything useful.
* It is an example of how to use the "special vertex" list.
* The vertices in this list will be highlighted in the GRAFO
* interface.
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
/* Here the GRAFO headers */
#include "../pgin.h"
#include "../graph.h"
#include "../list.h"
/* You have to fill the pgin struct with information about your plugins.
* Each position of the pgin struct is related with some function you
* have programed. Below one example where you programmed five functions:
*
* Pgin pgin[6] = {
* { PGIN_RESULT_ALG, "Find a Hamilton Path", "HPath", 0 },
* { PGIN_TEST_ALG, "Test Planarity", "PlanarGraph", 0 },
* { PGIN_TEST_ALG, "Test Bergeness", "BergeGraph", 0 },
* { PGIN_TRANSF, "Compute the complement", "Compl", PGIN_FLAG_NOREDRAW },
* { PGIN_TRANSF, "Line Graph", "LineGraph", 0 },
* { PGIN_LIST_END, NULL, NULL, 0 },
* };
*
* In the last position you should put { PGIN_LIST_END, NULL, NULL }, to
* end the list of plugins.
* You have to put four pieces of information in the pgin struct:
* -> The first is the class of your algorithm. The first entry
* above is a Result Algorithm, so you have to put PGIN_RESULT_ALG
* -> The second (in this case "Highest Degree") is the name that will
* appear in the menu of GRAFO.
* -> The third is the name of the function in the code (in this
* case "MaxDegree").
* -> The fourth is a set of plugin flags. In the example of the
* fouth funtion the flag prevents that GRAFO redraws the resulting graph.
* If you do not know what is a "plugin flag", only put 0 in this field.
*/
/* Plugin Information */
Pgin pgin[2] = {
{ PGIN_RESULT_ALG, "Highest Degree", "MaxDegree" },
{ PGIN_LIST_END, NULL, NULL },
};
/* The pgin_info() function should always be present. GRAFO will call
* it to get the plugin information.
*/
Pgin *pgin_info(void);
Pgin *pgin_info(void){
return pgin;
}
/* Plugin example: This program does not compute anything useful.
* It is an example of how to use the "special vertex" list.
* Here this list have the name verts. The vertices in this list will
* be highlighted in the GRAFO interface.
* In this example, the function finds the vertex with the highest
* degree (acctualy one of them) and put it in the verts list. */
int MaxDegree(Graph *G, char *mess, List *arc_edges, List *verts);
int MaxDegree(Graph *G, char *mess, List *arc_edges, List *verts){
Node N;
int i,maxdeg;
/* Test if graph is empty */
if (G->size < 1) {
sprintf(mess, "%s", "Empty graph!");
return 1;
}
/* Find the vertex with max degree */
maxdeg = 0;
for (i = 1; i < G->size; i++) {
if (G->vertex[i].degree > G->vertex[maxdeg].degree) {
maxdeg = i;
}
}
/* Place maxdeg in the Node */
N = MakeNode(&maxdeg, sizeof(int));
/* Place the node in the list of "special vertex" */
InsertNode(verts, N);
return 1;
}
/* ******* */
/* * End * */
/* ******* */
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 | /*
* grafo - graph editor
* Copyright (c) 2003-2008
* Murilo Vicente Goncalves da Silva <murilo@pet.inf.ufpr.br>
* Oliver Matias van Kaick <oliver@pet.inf.ufpr.br>
* Ulisses Cordeiro Pereira <ulisses@cordeiropereira.com.br>
*
* This program is free software; you can redistribute it and/or modify
* it under the terms of the GNU General Public License as published by
* the Free Software Foundation; either version 2 of the License, or
* (at your option) any later version.
*
* This program is distributed in the hope that it will be useful,
* but WITHOUT ANY WARRANTY; without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
* See the GNU General Public License for more details (file COPYING).
*/
/* ***************** */
/* * edgeexample.c * */
/* ***************** */
/* Plugin example: This program does not compute anything useful.
* It is an example of how to use the "special edge" list.
* The edges in this list will be highlighted in the GRAFO
* interface.
*
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
/* Here the GRAFO headers */
#include "../pgin.h"
#include "../graph.h"
#include "../list.h"
/* You have to fill the pgin struct with information about your plugins.
* Each position of the pgin struct is related with some function you
* have programed. Below one example where you programmed five functions:
*
* Pgin pgin[6] = {
* { PGIN_RESULT_ALG, "Find a Hamilton Path", "HPath", 0 },
* { PGIN_TEST_ALG, "Test Planarity", "PlanarGraph", 0 },
* { PGIN_TEST_ALG, "Test Bergeness", "BergeGraph", 0 },
* { PGIN_TRANSF, "Compute the complement", "Compl", PGIN_FLAG_NOREDRAW },
* { PGIN_TRANSF, "Line Graph", "LineGraph", 0 },
* { PGIN_LIST_END, NULL, NULL, 0 },
* };
*
* In the last position you should put { PGIN_LIST_END, NULL, NULL }, to
* end the list of plugins.
* You have to put four pieces of information in the pgin struct:
* -> The first is the class of your algorithm. The first entry
* above is a Result Algorithm, so you have to put PGIN_RESULT_ALG
* -> The second (in this case "Some Edge") is the name that will
* appear in the menu of GRAFO.
* -> The third is the name of the function in the code.
* -> The fourth is a set of plugin flags. In the example of the
* fouth funtion the flag prevents that GRAFO redraws the resulting graph.
*/
/* Plugin Information */
Pgin pgin[2] = {
{ PGIN_RESULT_ALG, "Some Edge", "MaxMinEdge",0 },
{ PGIN_LIST_END, NULL, NULL, 0 },
};
/* The pgin_info() function should always be present. GRAFO will call
* it to get the plugin information.
*/
Pgin *pgin_info(void);
Pgin *pgin_info(void){
return pgin;
}
/* The plugin example: It is an example of how to use the "special edge" list.
* Here the list have the name arc_edges. The edges in this list will
* be highlighted in the GRAFO interface.
*
* The following edge will be put in the list:
* Let the egde be called E. We will define it now: Let v be one vertex of the
* graph such that no other vertex has degree greater than v. Let
* u be the vertex adjacent to v with the lowest degree. The
* edge E links u to v. */
int MaxMinEdge(Graph *G, char *mess, List *arc_edges, List *verts);
int MaxMinEdge(Graph *G, char *mess, List *arc_edges, List *verts){
SEdge E; /* Single Edge */
Node N;
int i,maxdeg,mindeg;
/* Test if graph is empty */
if (G->size < 1) {
sprintf(mess, "%s", "Empty graph!");
return 1;
}
/* Find the vertex with max degree */
maxdeg = 0;
for (i = 1; i < G->size; i++) {
if (G->vertex[i].degree > G->vertex[maxdeg].degree) {
maxdeg = i;
}
}
/* Find the vertex with min degree adjacent with max degree */
mindeg = -1;
for (i = 0; i < G->size; i++) {
if (G->edge[maxdeg][i]) {
if (mindeg == -1) {
mindeg = i;
} else if (G->vertex[i].degree < G->vertex[mindeg].degree) {
mindeg = i;
}
}
}
/* Assign maxdeg and mindeg in a single edge */
E.u = maxdeg;
E.v = mindeg;
/* Place the "single edge" in the Node */
N = MakeNode(&E, sizeof(SEdge));
/* Place the node in the list of "special edges" */
InsertNode(arc_edges, N);
return 1;
}
/* ******* */
/* * End * */
/* ******* */
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 | /*
* grafo - graph editor
* Copyright (c) 2008
* Ulisses Cordeiro Pereira <ulisses@cordeiropereira.com.br>
*
* This program is free software; you can redistribute it and/or modify
* it under the terms of the GNU General Public License as published by
* the Free Software Foundation; either version 2 of the License, or
* (at your option) any later version.
*
* This program is distributed in the hope that it will be useful,
* but WITHOUT ANY WARRANTY; without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
* See the GNU General Public License for more details (file COPYING).
*/
/* ********************** */
/* * selectoddexample.c * */
/* ********************** */
/* Plugin example: This program does not compute anything useful.
* It is an example of how to use the "step by step" structure.
* The odd vertex and edges between odd vertex will be highlighted in the GRAFO
* interface.
*
*/
/* Plugin example: Select odd */
/* C language headers */
#include <stdio.h>
#include <stdlib.h>
/* Here the GRAFO headers */
/* Add plugins information */
#include "../pgin.h"
/* Add graph struct information */
#include "../graph.h"
/* Add step by step struct information */
#include "../step.h"
/* Mandatory function pgin_info */
Pgin *pgin_info(void);
/* algorithm function */
int SelectOdd(Graph *G, char *mess, int indx, List *arc_edges, List *verts);
/* Others functions */
/* The pgin_info() function should always be present. GRAFO will call
* it to get the plugin information.
*/
Pgin *pgin_info(void){
Pgin *pgin;
/* Alocate space for SelectOdd and PGIN_LIST_END */
pgin = (Pgin *) malloc(2 * sizeof(Pgin));
/* Includes SelectOdd as the first algorithm of plugin */
pgin[0].type = PGIN_STEP_ALG;
pgin[0].label = "Select odd";
pgin[0].name = "SelectOdd";
pgin[0].flags = 0;
/* It indicates the end of the list of algorithms */
pgin[1].type = PGIN_LIST_END;
pgin[1].label = 0;
pgin[1].name = 0;
pgin[1].flags = 0;
return pgin;
}
/* This is the plugin's main function */
int SelectOdd(Graph *G, char *mess, int indx, List *arc_edges, List *verts) {
SEdge E; /* Single Edge */
Node N;
int i, j,oddvertex;
/* Test if graph is empty */
if (G->size < 1) {
sprintf(mess, "%s", "Empty graph!");
return 1;
}
/* Set to False (0) the property 'mark' in all vertices */
ClearMarkedVerts(G);
/* Add first step - No highlights */
AddStep(G, arc_edges, verts);
/* Find and mark oddvertex */
oddvertex = 0;
for (i = 1; i < G->size; i++) {
/* Check if i is a odd number */
if ((i % 2)) {
/* Mark the vertex for future use */
G->vertex[i].mark = 1;
oddvertex = i;
/* Place oddvertex in the Node */
N = MakeNode(&oddvertex, sizeof(int));
/* Place the node in the list of "special vertex" */
InsertNode(verts, N);
/* Add new step - Save highlight vertex */
AddStep(G, arc_edges, verts);
}
}
/* Set to False (0) the property 'mark' in all vertices */
ClearMarkedEdges(G);
/* Find the odd vertex adjacent with other odd vertex */
for (i = 0; i < G->size; i++) {
for (j = 0; j < G->size; j++) {
/* Avoid saving the step [j,i] because [i,j] have been saved */
if (!G->prop[j][i].mark && \
/* True if vertex[i] is adjacent vertex[j] */
G->edge[i][j] && \
/* True if vertex[i] is a odd vertex */
G->vertex[i].mark && \
/* True if vertex[j] is a odd vertex */
G->vertex[j].mark) {
/* Mark the edge for future use */
G->prop[i][j].mark = 1;
/* Assign odd vertex adjacent with other odd vertex in a single edge */
E.u = i;
E.v = j;
/* Place the "single edge" in the Node */
N = MakeNode(&E, sizeof(SEdge));
/* Place the node in the list of "special edges" */
InsertNode(arc_edges, N);
/* Add new step - Save highlight edge */
AddStep(G, arc_edges, verts);
}
}
}
return 1;
}
/* ******* */
/* * End * */
/* ******* */
|