Problema A
Este problema pode ser resolvido notando-se que um ponto (cr,cc) de uma consulta está na janela que o contém que foi aberta por último, pois esta janela se sobrepõe às demais na região do ponto. Assim, basta verificar, dentre as janelas que contém o ponto (cr,cc), qual foi aberta por último.
Isto pode ser feito percorrendo-se a lista de janelas na ordem contrária a dada na entrada ("de trás para frente"), verificando se o ponto está na janela e parando o laço caso esteja. Alternativamente, é possível também percorrer a lista na ordem dada e atualizar a variável que contém a resposta sempre que o ponto está em uma janela. Um ponto (cr,cc) está em uma janela (r, c, w, h) se r <= cr <= r + h - 1 e c <= cc <= c + w - 1. Por fim, o ponto está em background se nenhuma janela o contém.
A complexidade desta solução é O(n*m).
Problema B
Resolver este problema requer mais experiência do que a necessária para resolver o restante desta prova. Não se assuste caso a solução descrita aqui é confusa ou impossível de se entender - isto será mais claro no futuro, com treino e prática. Esta solução utiliza conceitos da Teoria de Grafos e da técnica de Programação Dinâmica, temas que um maratonista irá encontrar durante seu treinamento em seu devido tempo, de maneira natural.
O grid dado na entrada é, na verdade, um grafo. Primeiramente, comprima os vértices de rótulo A em um único vértice. Isto é possível pois o enunciado garante que tais vértices formam um subgrafo conexo. Faça o mesmo com os vértices rotulados B, C e D.
O problema consiste agora em encontrar um subgrafo conexo mínimo que contém os 4 vértices, aqui chamados de "terminais". Esta é exatamente uma instância do problema (em grafos) da Árvore de Steiner.
Dentre outras maneiras, é possível resolver o problema com a técnica de Programação Dinâmica. Cada estado [u][S] consiste em um vértice u do grafo e um conjunto S de vértices terminais. A resposta do estado consiste no tamanho da menor árvore que contém o vértice u, e que conecta os vértices em S. A resposta do problema em si é dada então pela resposta, por exemplo, do estado [vA][{vB,vC,vD}], onde vi é o vértice rotulado i.
Para cada estado [u][S], caso S seja vazio, a resposta é 1, representando a árvore que contém apenas o vértice u. Se S contém apenas um vértice v, a resposta é o menor caminho entre v e u. Além disso, se u pertence a S, a resposta do estado [u][S] é igual a do estado [u][S-{u}].
A árvore buscada pode ser vista como a concatenação de duas subárvores T1 e T2, juntadas pelo vértice u. A figura abaixo exemplifica a situação. É importante notar que a árvore T1 conterá alguns vértices de S, enquanto T2 conterá os demais.
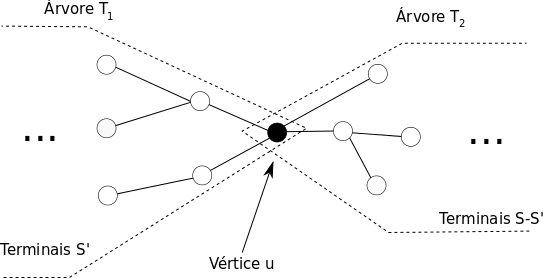
Assim, pode-se iterar em cada subconjunto próprio S' de S, representando que a árvore T1 tem os terminais em S', e a T2 os terminais em S-S', utilizando-se então a soma das respostas dos estados [u][S'] e [u][S-S'].
Ao invés de concatenar duas árvores, o vértice u também pode ser uma folha da árvore buscada. Neste caso, deve existir um caminho entre u e um vértice v na árvore tal que v age como um concatenador, como exemplifica a figura a seguir.
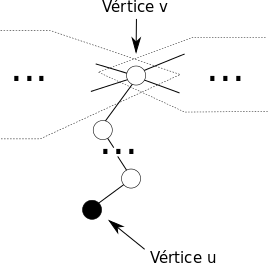
Assim, pode-se iterar em cada vértice v do grafo e atualizar a resposta do estado com o menor caminho entre u e v e o estado [v][S]. Para forçar que v seja um vértice concatenador, uma flag pode ser adicionada ao estado da PD. Assim, o estado passa a ser [u][S][F], onde F=0 ou F=1 indica se o vértice u deve necessariamente agir como um concatenador.
Por fim, ainda se u for considerado uma folha, um vértice terminal pode estar presente no caminho entre u e o vértice v. Nesse caso, atualiza-se também a resposta do estado com a soma do menor caminho entre u e cada vértice terminal t e a resposta do estado [t][S-{t}].
Essa técnica, de complexidade superestimada em O(34 * |V(G)|2), resolve este problema. É possível resolvê-lo de outras maneiras, entretanto. Por exemplo, é possível aproveitar-se do fato de que existem exatamente 4 vértices terminais na entrada para resolver este problema por força bruta, conhecendo-se a topologia de uma Árvore de Steiner geométrica de 4 vértices (basicamente, dois novos vértices são adicionados e todas suas combinações podem ser testadas, o que inclui alguns corner cases). Confira o código dos juízes deste problema nesta prova, e, apenas caso já se sinta confortável para isto, estude o problema da Árvore de Steiner.
Problema C
Note que uma string s é um anagrama de t (e, logo, t é um anagrama de s) se, para cada letra do alfabeto, ambas as strings têm o mesmo número de ocorrências da letra. Por exemplo, "BABA" é anagrama de "AABB" porque ambas as strings têm 2 As e 2 Bs. "ABBAC" não é anagrama de "CAABA" por que a primeira string tem 2 As, enquanto a segunda tem 3 As. Assim, o número de ocorrências da letra A em ambas as strings é diferente.
Assim, deve-se transformar a string s de tal forma que ela tenha a mesma quantidade de ocorrências da letra A, da letra B, etc da string t. Essa quantidade pode ser calcula varrendo-se a string t e mantendo um contador para cada letra.
Este problema pode ser resolvido com uma abordagem gulosa. Primeiramente, calcule, com um laço em s, o "saldo" de cada letra do alfabeto. O "saldo" de uma letra é dado pela diferença entre suas ocorrências em s e suas ocorrências em t. Assim, se existem, por exemplo, 3 Ds em s e 4 Ds em t, o "saldo" da letra D é igual a 3-4=-1. Note que uma letra de s está "sobrando" se seu saldo é positivo, está "faltando" se seu saldo é negativo, e está "ok" se seu saldo é zero.
Considere agora um laço que percorre a string s da esquerda para a direita. A cada passo, considere a letra s[i]. Se s[i] está faltando ou está "ok", ignore-a. Se ela estiver sobrando:
- Se existe alguma outra letra faltando que é lexicograficamente menor que s[i], troque s[i] pela menor letra que está faltando e atualize o saldo de ambas;
- Caso contrário, troque a letra s[i] apenas se você *realmente* precisa trocá-la, isto é, se o número de ocorrências de s[i] à direita da posição i é igual ao seu saldo. Por exemplo, se o saldo da letra é 4 e existem exatamente 4 ocorrências da letra a sua direita, todas as 4 deverão ser trocadas. Troque a letra pela letra lexicograficamente menor faltando (mesmo que ela seja maior que s[i]) e atualize o saldo de ambas;
- Caso contrário, ignore-a.
Ao final do laço, o saldo de todas as letras será 0 e, logo, s será um anagrama de t. Intuitivamente, o algoritmo funciona porque troca as letras que estão sobrando pelas que estão faltando. Como não há trocas "inúteis", o número de operações realizadas é mínimo. Além disso, o fato de se trocar as letras apenas quando há outra lexicograficamente menor faltando ou quando estritamente obrigatório garante que o anagrama gerado é o menor possível, lexicograficamente.
Esse algoritmo tem complexidade O(n), sendo n o tamanho das strings s e t.
Problema D
Para qualquer número inicial H <= 500, a sequência sempre gera o número 1 eventualmente. Além disso, o tamanho da sequência é pequeno o bastante, de forma que é possível simplismente gerá-la toda.
Assim, execute um laço mantendo o número anterior da sequencia e atualizando-o de acordo com a definição da mesma, parando-o quando o número for igual a 1. Mantenha uma variável para a reposta que é inicializada com H e é atualizada sempre que o número gerado for maior que ela.
Essa solução tem complexidade O(|h(H)|), onde |h(H)| é igual ao tamanho da sequência gerada, iniciada em H.
Problema E
Vide editorial do 1º treino.
Problema F
Este problema poderia ser resolvido iterando-se em cada tripla de pontos, calculando a distância entre eles e verificando se duas delas são iguais. Esta solução, entretanto, tem complexidade O(n3), e é muito lenta para este problema.
Em um triângulo isósceles, sempre existe um ponto P que está na extremidade de ambos os lados cujos comprimentos são iguais. No triângulo formado pelos pontos (0,0), (0,1) e (1,0), por exemplo, P = (0,0), por este ponto estar tanto no lado (0,0)-(0,1) quanto no lado (0,0)-(1,0), ambos de tamanho 1. Para facilitar a compreensão, os outros pontos do triangulo são aqui chamados de A e B.
Para cada ponto (x,y) da entrada, calcula-se a quantidade de triângulos isósceles em que P=(x,y). Note que tal quantidade é igual ao número de pares A, B de pontos cuja distância de A a P é igual à distância de B a P. Assim, basta construir um vetor contendo a distância de todos os pontos da entrada ao ponto (x,y) e verificar quantas ocorrências repetidas ocorrem neste vetor. Para cada distância que ocorre k vezes neste vetor, soma-se na resposta a combinação de k dois a dois, pois quaisquer dois pontos com a mesma distância de P formam um triângulo isósceles. Note que, como o enunciado do problema garante a inexistência de triângulos equiláteros, nenhum triângulo está sendo contado mais de uma vez.
Esta conta pode ser realizada, por exemplo, ordenando-se o vetor (de forma que ocorrências repetidas estão em posições consecutivas) e varrendo-o, mantendo um contador de ocorrências do elemento atual.
Se um método O(n log n) for utilizado para se ordenar o vetor (como a função
sort() que está disponível para uso na biblioteca