Trabalho 1: Regressão Linear

Neste exercício, você irá implementar a regressão linear e ver como ela funciona com dados.

Você precisará baixar o código inicial e descompactar o conteúdo no diretório onde deseja.

Arquivos incluídos

O símbolo [*] indica os arquivos que você precisará completar.

Ao longo do exercício, você usará os scripts ex1.py e ex1_multi.py. Esses scripts preparam o conjunto de dados para os problemas e fazem chamadas para as funções que você escreverá. Você não precisa modificar nenhum deles. Você só precisa modificar as funções em outros arquivos, seguindo as instruções desta tarefa.

Para este exercício de programação, você precisa completar a primeira parte, que implementa a regressão linear com uma variável, e a segunda parte, aborda a regressão linear com múltiplas variáveis.

Observação: Para os exercícios de programação, você usará principalmente a biblioteca NumPy. Certifique-se de importá-la com import numpy as np.

Parte 1: Regressão Linear com uma Variável

Nesta parte do exercício, você implementará a regressão linear com uma variável para prever os lucros de um food truck. Suponha que você é o CEO de uma franquia de restaurantes e está considerando diferentes cidades para abrir uma nova filial. A rede já possui food trucks em várias cidades e você tem dados de lucros e populações dessas cidades. Você gostaria de usar esses dados para ajudar a escolher a próxima cidade para expandir.

O arquivo ex1data1.txt contém o conjunto de dados para o nosso problema de regressão linear. A primeira coluna é a população de uma cidade e a segunda coluna é o lucro de um food truck nessa cidade. Um valor negativo para o lucro indica prejuízo. O script ex1.py já foi configurado para carregar esses dados para você.

1.1 - Plotando os Dados

Antes de começar qualquer tarefa, é frequentemente útil entender os dados visualizando-os. Para este conjunto de dados, você pode usar um gráfico de dispersão (scatter plot) para visualizá-lo, já que ele tem apenas duas propriedades para plotar (lucro e população).

Em ex1.py, o conjunto de dados é carregado do arquivo de dados para as variáveis X e y:
data = np.loadtxt('ex1data1.txt', delimiter=',', usecols=(0, 1))
X = data[:, 0]
y = data[:, 1]
m = y.size

Em seguida, o script chama a função plot_data(x, y) para criar um gráfico de dispersão dos dados. Sua tarefa é completar plotData.py para desenhar o gráfico. Você pode usar a biblioteca Matplotlib para isso. Modifique o arquivo e preencha o seguinte código:
plt.scatter(x, y, marker='x', c='r', s=100)
plt.ylabel('Profit in $10,000s')
plt.xlabel('Population of City in 10,000s')
plt.show()

Agora, ao continuar a executar ex1.py, o resultado final deverá ser semelhante à Figura 1, com os mesmos marcadores “x” vermelhos e rótulos de eixo. Para saber mais sobre o comando scatter e outros comandos de plotagem, você pode pesquisar online pela documentação do Matplotlib.

Fig

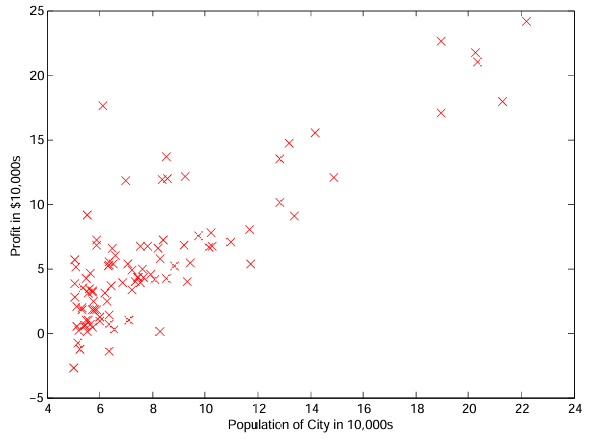
Figura 1: Gráfico de dispersão dos dados de treinamento

1.2 - Gradiente Descendente

Nesta parte, você ajustará os parâmetros da regressão linear θθ ao nosso conjunto de dados usando o gradiente descendente.

Equações de Atualização

O objetivo da regressão linear é minimizar a função de custo J(θ)J(θ).
J(θ)=12m∑i=1m(hθ(x(i))−y(i))2J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2onde a hipótese hθ(x)h_\theta(x) é dada pelo modelo linear:hθ(x)=θTx=θ0+θ1x1h_\theta(x) = \theta^T x = \theta_0 + \theta_1 x_1

Lembre-se que os parâmetros do seu modelo são os valores θjθ_j. Estes são os valores que você ajustará para minimizar o custo J(θ)J(θ). Uma maneira de fazer isso é usar o algoritmo de gradiente descendente em lote (batch gradient descent). Em cada iteração do gradiente descendente em lote, a atualização é realizada:
θj:=θj−α1m∑i=1m(hθ(x(i))−y(i))xj(i)\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}
(atualize θjθ_j simultaneamente para todos os jj).

A cada passo do gradiente descendente, seus parâmetros θjθ_j se aproximam dos valores ideais que alcançarão o custo mais baixo J(θ)J(θ).

Nota de Implementação: Armazenamos cada exemplo como uma linha na matriz X no NumPy. Para levar em conta o termo de interceptação (θ0θ_0), adicionamos uma primeira coluna a X e a definimos como todos uns. Isso nos permite tratar θ0θ_0 simplesmente como outro “recurso”.

Implementação

Em ex1.py, já configuramos os dados para a regressão linear. Nas linhas seguintes, adicionamos outra dimensão aos nossos dados para acomodar o termo de interceptação θ0θ_0. Também inicializamos os parâmetros iniciais para 0 e a taxa de aprendizado alpha para 0.01.
X = np.c_[np.ones(m), X]
theta = np.zeros(2)
iterations = 1500
alpha = 0.01

Calculando o Custo J(θ)J(θ)

Ao realizar o gradiente descendente para aprender a minimizar a função de custo J(θ)J(θ), é útil monitorar a convergência calculando o custo. Nesta seção, você implementará uma função para calcular J(θ)J(θ) para que possa verificar a convergência de sua implementação do gradiente descendente.

Sua próxima tarefa é completar o código no arquivo computeCost.py, que é uma função que calcula J(θ)J(θ). Ao fazer isso, lembre-se que as variáveis X e y não são valores escalares, mas sim arrays NumPy cujas linhas representam os exemplos do conjunto de treinamento.

Depois de completar a função, o próximo passo em ex1.py executará computeCost uma vez usando θθ inicializado com zeros, e você verá o custo impresso na tela. Você deve esperar um custo de 32.07.

Gradiente Descendente

Em seguida, você implementará o gradiente descendente no arquivo gradientDescent.py. A estrutura do loop já foi escrita para você, e você só precisa fornecer as atualizações para θθ dentro de cada iteração. Ao programar, certifique-se de entender o que você está tentando otimizar e o que está sendo atualizado. Lembre-se que o custo J(θ)J(θ) é parametrizado pelo vetor θθ, não por X e y. Ou seja, nós minimizamos o valor de J(θ)J(θ) alterando os valores do vetor θθ, não alterando X ou y. Consulte as equações neste documento e nas videoaulas se tiver dúvidas.

Uma boa maneira de verificar se o gradiente descendente está funcionando corretamente é observar o valor de J(θ)J(θ) e verificar se ele está diminuindo a cada passo. O código inicial para gradientDescent.py chama computeCost a cada iteração e imprime o custo. Assumindo que você implementou o gradiente descendente e computeCost corretamente, seu valor de J(θ)J(θ) nunca deverá aumentar, e deverá convergir para um valor estável no final do algoritmo.

Depois de terminar, ex1.py usará seus parâmetros finais para plotar o ajuste linear. O resultado deve ser semelhante à Figura 2.

Seus valores finais para θθ também serão usados para fazer previsões de lucros em áreas de 35.000 e 70.000 pessoas. Note a forma como as seguintes linhas em ex1.py usam a multiplicação de matrizes, em vez de somas ou loops explícitos, para calcular as previsões. Este é um exemplo de vetorização de código em Python/NumPy.
predict1 = np.dot([1, 3.5], theta)
predict2 = np.dot([1, 7], theta)

1.3 - Depuração

Aqui estão algumas coisas a ter em mente ao implementar o gradiente descendente:

Fig

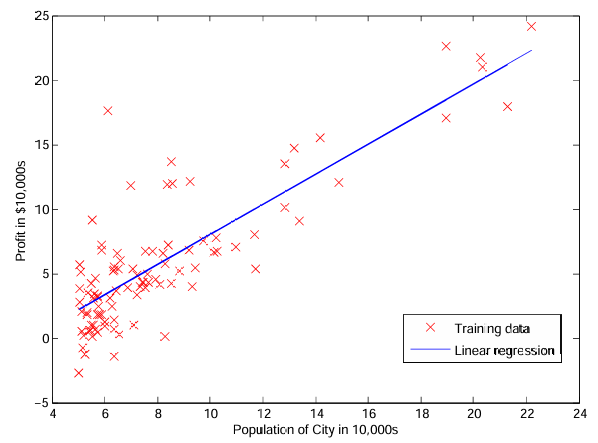
Figura 2: Dados de treinamento com ajuste de regressão linear

1.4 - Visualizando J(θ)J(θ)

Para entender melhor a função de custo J(θ)J(θ), você irá agora plotar o custo em uma grade bidimensional dos valores de θ_0θ\_0 e θ_1θ\_1. Você não precisará codificar nada de novo para esta parte, mas deve entender como o código que você já escreveu está criando essas imagens.

Na próxima etapa de ex1.py, há um código configurado para calcular J(θ)J(θ) em uma grade de valores usando a função computeCost que você escreveu.

for i in range(0, theta0_vals.size):
for j in range(0, theta1_vals.size):
t = np.array([theta0_vals[i], theta1_vals[j]])
J_vals[i][j] = compute_cost(X, y, t)

Após a execução dessas linhas, você terá uma matriz 2D de valores de J(θ)J(θ). O script ex1.py usará esses valores para produzir gráficos de superfície e de contorno de J(θ)J(θ) usando as funções plot_surface e contour do Matplotlib. Os gráficos devem ser semelhantes à Figura 3.

Fig

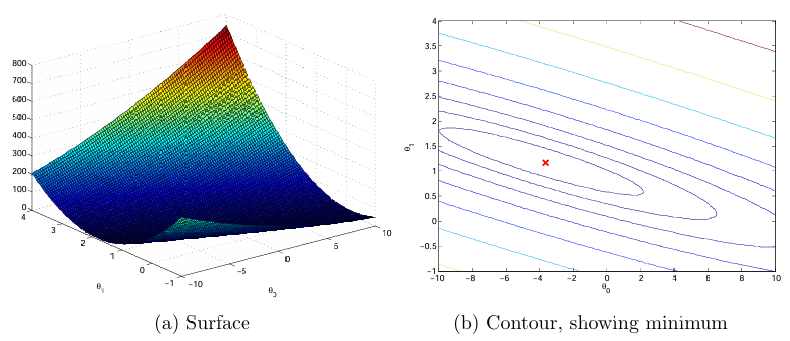
Figura 3: Função de Custo J(θ)

O objetivo desses gráficos é mostrar como J(θ)J(θ) varia com as mudanças em θ_0θ\_0 e θ_1θ\_1. A função de custo J(θ)J(θ) tem forma de tigela e possui um mínimo global. (Isso é mais fácil de ver no gráfico de contorno do que no gráfico de superfície 3D). Este mínimo é o ponto ideal para θ_0θ\_0 e θ_1θ\_1, e cada passo do gradiente descendente se move para mais perto deste ponto.

Parte 2 - Regressão Linear com Múltiplas Variáveis

Nesta parte, você implementará a regressão linear com múltiplas variáveis para prever os preços de casas. Suponha que você está vendendo sua casa e quer saber qual seria um bom preço de mercado. Uma maneira de fazer isso é primeiro coletar informações sobre casas vendidas recentemente e criar um modelo de preços de moradia.

O arquivo ex1data2.txt contém um conjunto de treinamento de preços de moradias em Portland, Oregon. A primeira coluna é o tamanho da casa (em pés quadrados), a segunda coluna é o número de quartos e a terceira coluna é o preço da casa. O script ex1_multi.m foi configurado para ajudá-lo a seguir este exercício.

2.1 - Normalização de Características (Features)

O script ex1_multi.py começará carregando e exibindo alguns valores deste conjunto de dados. Ao observar os valores, note que os tamanhos das casas são cerca de 1000 vezes o número de quartos. Quando os recursos diferem por ordens de magnitude, a aplicação de escalonamento de recursos (feature scaling) pode fazer com que o gradiente descendente convirja muito mais rapidamente.

Sua tarefa aqui é completar o código em featureNormalize.py para:

O desvio padrão é uma forma de medir a variação na gama de valores de um recurso específico. No NumPy, você pode usar a função np.std para calcular o desvio padrão. Por exemplo, dentro de featureNormalize.py, o array X[:, 0] contém todos os valores de x1x_1 (tamanhos das casas) no conjunto de treinamento, então np.std(X[:, 0]) calcula o desvio padrão dos tamanhos das casas.

No momento em que featureNormalize.py é chamado, a coluna extra de 1s correspondente a x0=1x_0=1 ainda não foi adicionada a X. Você fará isso para todos os recursos e seu código deve funcionar com conjuntos de dados de todos os tamanhos (qualquer número de recursos/exemplos). Observe que cada coluna da matriz X corresponde a um recurso.

Nota de Implementação: Ao normalizar os recursos, é importante armazenar os valores usados para a normalização - o valor médio e o desvio padrão usados para os cálculos. Depois de aprender os parâmetros do modelo, muitas vezes queremos prever os preços de casas que não vimos antes. Dado um novo valor x (área da sala de estar e número de quartos), devemos primeiro normalizar x usando a média e o desvio padrão que havíamos calculado anteriormente a partir do conjunto de treinamento.

2.2 - Gradiente Descendente

Anteriormente, você implementou o gradiente descendente em um problema de regressão univariada. A única diferença agora é que há uma característica a mais na matriz X. A função de hipótese e a regra de atualização do gradiente descendente em lote permanecem inalteradas.

Você deve completar o código em gradientDescent.py para implementar o gradiente descendente para regressão linear com múltiplas variáveis. Se seu código na parte anterior (variável única) já suporta múltiplas variáveis, você pode usá-lo aqui também. Certifique-se de que seu código suporta qualquer número de características e é bem vetorizado. Você pode usar X.shape[1] para descobrir quantas características estão presentes no conjunto de dados.

Nesta parte do exercício, você poderá experimentar diferentes taxas de aprendizado para o conjunto de dados e encontrar uma taxa de aprendizado que converge rapidamente. Você pode alterar a taxa de aprendizado modificando ex1_multi.py e alterando a parte do código que define a taxa de aprendizado.

A próxima fase em ex1_multi.py chamará sua função gradientDescent.py e executará o gradiente descendente por cerca de 50 iterações na taxa de aprendizado escolhida. A função também deve retornar o histórico dos valores de J(θ)J(θ) em um array J. Após a última iteração, o script ex1_multi.py plota os valores de J em relação ao número de iterações. Se você escolheu uma taxa de aprendizado dentro de um bom intervalo, seu gráfico será semelhante à Figura 4. Se seu gráfico parecer muito diferente, especialmente se o valor de J(θ)J(θ) aumentar ou até “explodir”, ajuste sua taxa de aprendizado e tente novamente. Nós recomendamos tentar valores da taxa de aprendizado αα em uma escala logarítmica, em passos multiplicativos de cerca de 3 vezes o valor anterior (ou seja, 0.3, 0.1, 0.03, 0.01 e assim por diante).

Fig

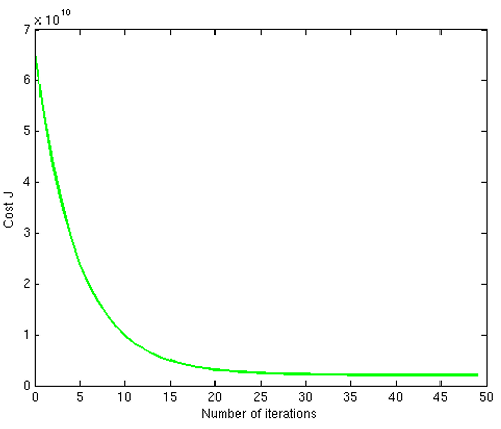
Figura 4: Convergência do gradiente descendente com uma taxa de aprendizado apropriada

Dica de Python: Para comparar como diferentes taxas de aprendizado afetam a convergência, é útil plotar JJ para várias taxas de aprendizado no mesmo gráfico. No Matplotlib, isso pode ser feito executando o gradiente descendente várias vezes e chamando plt.plot() para cada resultado. Concretamente, se você tentou três valores diferentes de alpha e armazenou os custos em J1, J2 e J3, você pode usar os seguintes comandos para plotá-los no mesmo gráfico:
plt.plot(range(50), J1[:50], c='b')
plt.plot(range(50), J2[:50], c='r')
plt.plot(range(50), J3[:50], c='k')
plt.show()

Nota de Implementação: Se sua taxa de aprendizado for muito grande, J(θ)J(θ) pode divergir e “explodir”, resultando em valores que são muito grandes para cálculos de computador. Nessas situações, o Python tenderá a retornar np.inf ou np.nan. np.nan significa “not a number” (não é um número) e é frequentemente causado por operações indefinidas que envolvem inf.

Observe as mudanças nas curvas de convergência à medida que a taxa de aprendizado muda. Com uma taxa de aprendizado pequena, você deve descobrir que o gradiente descendente leva muito tempo para convergir para o valor ideal. Por outro lado, com uma taxa de aprendizado grande, o gradiente descendente pode não convergir ou pode até divergir!

Usando a melhor taxa de aprendizado que você encontrou, execute o script ex1_multi.py para executar o gradiente descendente até a convergência para encontrar os valores finais de θθ. Em seguida, use este valor de θθ para prever o preço de uma casa com 1650 pés quadrados e 3 quartos. Você usará esse valor mais tarde para verificar sua implementação das equações normais. Não se esqueça de normalizar suas características ao fazer esta previsão!

Avaliação

A seguir, um detalhamento de como cada parte deste exercício é pontuada.

Parte Arquivo Submetido Pontos
Plotagem plotData.py 10 pontos
Calcular custo para uma variável computeCost.py 30 pontos
Gradiente descendente para uma e múltiplas variáveis gradientDescent.py 40 pontos
Normalização de recursos featureNormalize.py 20 pontos
Pontos Totais 100 pontos