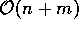Até agora tratamos de problemas simples, mas a Geometria Computacional, embora seja atraente, com muitas técnicas, também tem problemas difí ceis. Problemas como o de achar a intersecção de dois poliédros convexos pode parecer fácil, mas se o objetivo é achar o algoritmo ótimo, então começa a complicar.
O artigo [Cha89], de Chazelle, estuda o problema acima, e afirma
existir um algoritmo de complexidade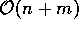 
, onde n e m são
os tamanhos dos dois polí gonos. Este algoritmo usa e abusa de dualidade,
fecho convexo, triangulação de Delaunay (3D no caso). Não apresenta
uma implementação, pois é muito teórico.
Um outro problema difí cil é o de montagem/desmontagem de objetos formados por n peças. Este problema foi estudado por Stolfi, e tem uma de suas soluções\ efetuando-se a subdivisão de um espaço de dimensão 5, no qual estão representados os movimentos que cada peça pode fazer.
Estes dois problemas são exemplos de como podemos complicar a vida de quem procura soluções ótimas para problemas simples.