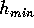 e
e 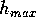 , idade entre
, idade entre 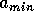 e
e 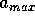 e
salário entre
e
salário entre 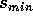 e
e 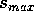 , como resolver?
, como resolver?
Muitos algoritmos precisam de estruturas de dados eficientes para que possam executar suas tarefas no tempo esperado. Vejamos então algumas destas estruturas. Daremos ênfase às estruturas hierárquicas, visto que são as mais comuns além, é claro, das listas.
Normalmente uma hierarquia é representada por uma árvore, o que também tem muita relação com os algoritmos recursivos.
Uma generalização das árvores binárias de busca, para dimensões maiores é a árvore k-d, ou k-dimensional. Esta árvore é uma árvore binária, mas a cada ní vel a chave de busca é trocada.
Suponha que temos um banco de dados com o nome, salário, idade, e altura dos
funcionários de uma firma. Se quisermos saber quais os funcionários que
tem altura entre 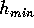 e
e 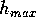 , idade entre
, idade entre 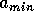 e
e 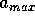 e
salário entre
e
salário entre 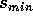 e
e 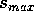 , como resolver?
, como resolver?
Seja T uma árvore binária com todos os registros do banco de dados, de forma que no ní vel 0 (raiz) a chave é o salário, no ní vel 1, é a idade, no ní vel 3, a altura, e no ní vel 4 voltamos ao salário.
Assim, podemos saber quais os registros que satisfazem à restrição acima fazendo algumas buscas binárias. Na verdade posso precisar descer por dois ramos da árvore, e o algoritmo tem pior caso linear (pois todos os registros podem estar na resposta). Perceba que a árvore deve estar balanceada.
Vejamos um exemplo no plano. Dado um conjunto 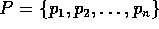 com
n pontos no plano, (veja figura 3.2), vamos construir uma
árvore 2-d e usá-la para resolver o problema de saber quais destes pontos
está dentro de uma região retangular R.
com
n pontos no plano, (veja figura 3.2), vamos construir uma
árvore 2-d e usá-la para resolver o problema de saber quais destes pontos
está dentro de uma região retangular R.
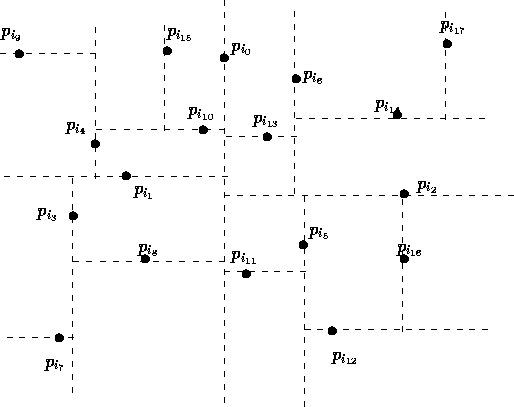
Figure: Construção da árvore 2-d
Ordene os pontos por uma de suas coordenadas, digamos x, e escolha a mediana
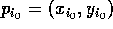 . Este ponto será a raí z da árvore. Sejam
. Este ponto será a raí z da árvore. Sejam 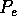 e
e 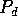 dois subconjuntos de P tais que
dois subconjuntos de P tais que 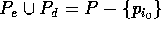 , e os pontos com
coordenada x menor ou igual a
, e os pontos com
coordenada x menor ou igual a 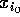 estão em
estão em 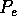 , e os com coordenada x maior
que
, e os com coordenada x maior
que 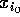 , em
, em 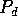 . Estes dois conjuntos serão as sub-árvores esquerda (
. Estes dois conjuntos serão as sub-árvores esquerda ( 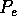 ) e
direita (
) e
direita ( 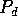 ) de
) de 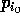 .
.
Repita este processo, escolhendo a proxima coordenada, no caso y, para os
conjuntos 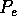 e
e 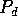 , montando assim a árvore T da figura 3.3
em tempo
, montando assim a árvore T da figura 3.3
em tempo 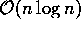 . Você consegue explicar o motivo desta complexidade?
. Você consegue explicar o motivo desta complexidade?
Com a árvore construí da, passemos para o problema. Dada uma região R do plano, enumerar os pontos do conjunto P que estão no interior de R. O que faremos é descer na árvore decidindo se cada ponto no caminho está no interior de R, e se algum dos lados da árvore pode ser descartado. Suponha que a variável R tenha dois campos, menor e maior, cada um sendo um vetor de duas posições, representando os dois pontos extremos de R, inferior esquerdo e superior direito. Suponha também que os nós da árvore são estruturas, que além dos ponteiros esq e dir, têm o campo ponto que é o ponto propriamente dito.
Apresentaremos o procedimento Busca que recebe o raí z de uma árvore, um í ndice da coordenada usada como chave (1 para x e 2 para y), e a região R, e tem como saí da o conjunto de pontos da árvore que estão no interior de R.
O procedimento é o seguinte:
Busca ( v, chave, R )
*
{
*
/* c'alculo da outra chave */
*
outra  3 - chave;
*
se v.ponto[chave] < R.menor[chave] então
*
Busca ( v.dir, outra, R );
*
senão
*
{
*
se v.ponto[chave] > R.maior[chave] então
*
Busca ( v.esq, outra, R );
*
senão
*
{
*
/* se o ponto est'a dentro de R */
*
se (v.ponto[outra]
3 - chave;
*
se v.ponto[chave] < R.menor[chave] então
*
Busca ( v.dir, outra, R );
*
senão
*
{
*
se v.ponto[chave] > R.maior[chave] então
*
Busca ( v.esq, outra, R );
*
senão
*
{
*
/* se o ponto est'a dentro de R */
*
se (v.ponto[outra] 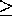 R.menor[outra])
*
& (v.ponto[outra]
R.menor[outra])
*
& (v.ponto[outra] 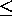 R.maior[outra]) então
*
inclua v na resposta;
*
Busca ( v.esq, outra, R );
*
Busca ( v.dir, outra, R );
*
}
*
}
*
}
R.maior[outra]) então
*
inclua v na resposta;
*
Busca ( v.esq, outra, R );
*
Busca ( v.dir, outra, R );
*
}
*
}
*
}
Para resolver o nosso problema, basta executar Busca ( Raí z(T), 1, R ), onde Raí z(T) retorna o ponteiro para o nó raí z da árvore T.