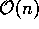 , então o
algoritmo tem complexidade
, então o
algoritmo tem complexidade 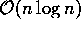 . E se esses procedimentos tem
complexidade
. E se esses procedimentos tem
complexidade 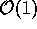 , então o
algoritmo tem complexidade
, então o
algoritmo tem complexidade 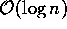 .
.
Esta técnica é muito usada em toda ciência da computação. Um exemplo bastante conhecido é o algoritmo para ordenação quicksort, que pode ser encontrado em quase todos os livros sobre algoritmos. O algoritmo para achar o fecho convexo de um conjunto de pontos no plano apresentado na seção 2.3 é outro exemplo.
A base desta técnica é a recursão, dividindo o problema em duas instâncias menores, resolvendo estas instâncias recursivamente e depois agrupando as soluções.
Um fato bastante importante diz respeito à complexidade de algoritmos que usam esta técnica:
Se um certo problema é dividido exatamente ao meio em um algoritmo com a técnica dividir-para-conquistar e os procedimentos para a divisão e unificação juntos têm complexidade, então o algoritmo tem complexidade
. E se esses procedimentos tem complexidade
, então o algoritmo tem complexidade
.