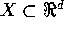 é a menor região
convexa do
é a menor região
convexa do 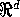 que contém o conjunto X.
que contém o conjunto X.
O fecho convexo FC(X) de um conjunto 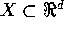 é a menor região
convexa do
é a menor região
convexa do 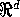 que contém o conjunto X.
que contém o conjunto X.
Achar o fecho convexo de um conjunto de pontos, por exemplo, é um problema que aparece quando queremos organizar o conjunto, agrupar os pontos em uma região simples.
Em quase todos os casos o conjunto X, do qual se quer obter o fecho convexo FC(X), é um conjunto finito de pontos, e o fecho convexo será um politopo (veja figura 2.5).
Como um politopo pode ser representado? Em dimensão 2, temos um polí gono, que pode ser descrito por uma lista ordenada (no sentido anti-horário, por exemplo) de seus vértices. Em dimensão 3, temos um poliédro, que precisa de estruturas um pouco mais complicadas para armazenar as faces que compõem a fronteira.
Em dimensões maiores, as coisas se complicam ainda mais, pois precisariamos de estruturas que representassem as faces de todas as dimensões.
Uma aplicação interessante para o fecho convexo seria na melhor organização\
dos pontos no problema anterior, onde querí amos saber qual o ponto do conjunto
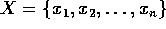 mais próximo
de um certo ponto p.
Se o ponto p está no interior de FC(X), usamos o algoritmo que discutimos
na seção\
anterior (com ou sem pré-processamento), se estiver fora, o ponto mais próximo
será um dos vértices de FC(X).
mais próximo
de um certo ponto p.
Se o ponto p está no interior de FC(X), usamos o algoritmo que discutimos
na seção\
anterior (com ou sem pré-processamento), se estiver fora, o ponto mais próximo
será um dos vértices de FC(X).
Perceba que precisamos usar aqui o algoritmo para saber se um certo ponto está no interior de um polí gono.
O fecho convexo pode ser definido como o conjunto das combinações convexas dos
pontos de 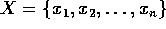 .
.
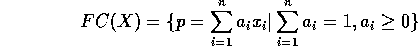
A fronteira 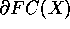 de FC(X) é o conjunto onde no máximo d
í ndices são maiores que zero, onde n é a dimensão do espaço.
de FC(X) é o conjunto onde no máximo d
í ndices são maiores que zero, onde n é a dimensão do espaço.
E como construir o fecho convexo de um conjunto 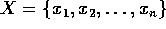 de pontos do plano?
de pontos do plano?
Dividindo o conjunto X em dois usando uma reta vertical, por exemplo,
que passe no meio dos pontos, teremos os conjuntos 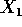 e
e 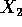 . Se
calcularmos os fechos
. Se
calcularmos os fechos 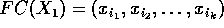 e
e
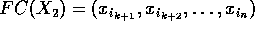 de
de 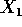 e
e 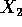 ,
ambos ordenados no sentido anti-horário, o fecho convexo
de X pode ser calculado como parte dos dois fechos mais duas novas
arestas, que chamaremos de pontes. Veja na figura 2.6.
Assim, calculamos os dois fechos,
,
ambos ordenados no sentido anti-horário, o fecho convexo
de X pode ser calculado como parte dos dois fechos mais duas novas
arestas, que chamaremos de pontes. Veja na figura 2.6.
Assim, calculamos os dois fechos, 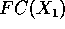 e
e 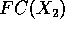 , recursivamente,
até que tenham 3 ou menos vértices (quando o fecho é trivial). Só
resta saber como achar as pontes.
, recursivamente,
até que tenham 3 ou menos vértices (quando o fecho é trivial). Só
resta saber como achar as pontes.
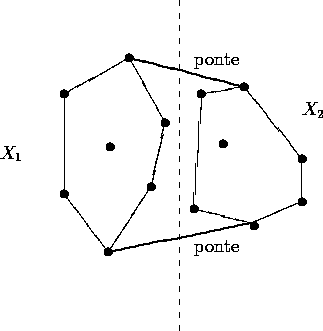
Figure: Pontes para construção do fecho convexo
Estas pontes podem ser encontradas facilmente a partir de aproximações
sucessivas. Escolhemos os pontos mais próximos da reta, um de cada lado,
digamos 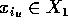 e
e 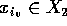 , e elevamos (descemos) o segmento
, e elevamos (descemos) o segmento
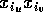 ,
ora trocando o primeiro, ora trocando o segundo (veja figura 2.7).
,
ora trocando o primeiro, ora trocando o segundo (veja figura 2.7).
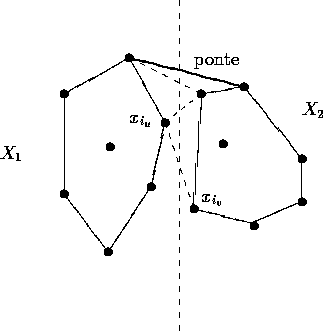
Figure 2.7: Algoritmo para encontrar as pontes
O algoritmo seria o seguinte:
Faça a= u e b = v;Repita
Enquanto o ângulo do segmento
para o segmento
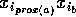
for no sentido hor'ario faça
;
Enquanto o ângulo do segmento
para o segmento
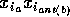
for no sentido anti-hor'ario faça
;
at'e que não ocorra mudanças;
Onde a operação prox em a retorna o próximo vértice, e ant em b, o anterior na lista de vértices, que deve ser considerada circular.
O segmento 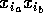 resultante é uma das pontes.
Faça a mesma coisa para a outra ponte, sendo que a = v e b = u.
resultante é uma das pontes.
Faça a mesma coisa para a outra ponte, sendo que a = v e b = u.
Desta forma teremos complexidade 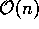 para calcular as pontes, já que
percorreremos os vértices dos fechos
para calcular as pontes, já que
percorreremos os vértices dos fechos 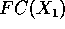 e
e 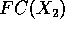 no máximo 3 vezes
(uma para achar os pontos mais próximos da reta, e uma para cada ponte).
no máximo 3 vezes
(uma para achar os pontos mais próximos da reta, e uma para cada ponte).
Como o algoritmo se baseia na divisão do problema em dois menores e depois
unifica as soluções, a complexidade final fica 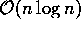 se as
divisões forem sempre próximas da metade. No pior caso, quando as divisões
são totalmente desproporcionais, a complexidade sobe para
se as
divisões forem sempre próximas da metade. No pior caso, quando as divisões
são totalmente desproporcionais, a complexidade sobe para 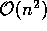 .
.
Este comportamento é semelhante ao algoritmo de ordenação quicksort.
Existem diversos outros algoritmos para resolver este problema, mas devido à
semelhança com ordenação, o limite mí nimo para este problema é
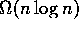 . Para referência a um outro algoritmo, veja [Pre79].
. Para referência a um outro algoritmo, veja [Pre79].