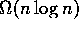Conhecida também como redução , esta técnica se baseia na redução de um problema em outro, utilizando transformações geométricas.
Uma equivalência interessante existe entre calcular a triangulação de Delaunay e o fecho convexo 3D de pontos sobre a superfí cie de um parabolóide (veja [GS89]).
Um outro exemplo mais simples é entre ordenação de números reais e o fecho convexo 2D de pontos sobre uma parábola (veja [FC91]).
Com esta técnica podemos descobrir limites inferiores para a complexidade de
alguns algoritmos, como por exemplo o de fecho convexo. Como o fecho convexo resolve
o problema da ordenação, que tem limite inferior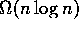 
, então
não pode ter complexidade menor que isso.