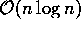Muitas estruturas possuem uma espécie de inversa, como os números reais, as matrizes, e etc. Esta dualidade, como é chamada, pode se apresentar de diversas formas. Suas caracterí sticas são tais que o dual de um objeto (primal) deve ter estrutura semelhante, e o dual do dual é o primal.
Esta técnica já é usada há muito tempo, por exemplo em programação linear, onde podemos resolver o problema dual ao invés do primal.
Aqui apresentaremos o Diagrama de Voronoi como sendo o dual da Triangulação\ de Delaunay. Normalmente o Diagrama de Voronoi é apresentado primeiro.
Se em cada circuncentro de cada triângulo da Triangulação de Delaunay for colocado um vértice, e entre cada par de novos vértices que estiverem em triângulos vizinhos, for colocada uma aresta coincidente com a mediatriz, teremos o Diagrama de Voronoi do conjunto de pontos iniciais.
Como visto na seção 2.2, o Diagrama de Voronoi divide o plano em regiões onde o ponto mais próximo de todos dentro de cada uma é o ponto inicial que está dentro dela.
O Diagrama de Voronoi é bastante útil, e pode ser encontrado facilmente através
da Triangulação de Delaunay, em tempo linear, portanto preciso de tempo
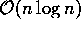para achá-lo.
Outra dualidade interessante é a de polí gonos. Seja um polí gono P de vértices
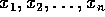. O polí gono Dual(P), dual de P, é tal que seus vértices
são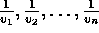 
, onde 
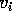é o ponto da
aresta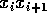 
mais próximo da origem (considere 
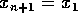), ou seja,
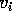é perpendicular à aresta 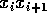com módulo igual a distância dela a
origem.
Um resultado bastante surpreendente, que usa a dualidade é o seguinte:
Sejam P e Q dois polí gonos planares, Dual o operador de dualidade como descrito acima, e FC o operador de fecho convexo, então
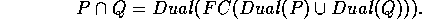
Este resultado nos diz que para calcular a intersecção de dois polí gonos, posso calcular o fecho convexo de seus duais, e depois dualizar. Como achar o dual é linear, temos uma relação entre intersecção de polí gonos e o fecho convexo no plano.