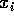 , com
, com 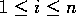 ,
e um ponto destino p, dizer qual o ponto
,
e um ponto destino p, dizer qual o ponto 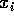 mais próximo de p.
mais próximo de p.
Este problema aparece, por exemplo, quando temos uma carta com um certo endereço destino, e precisamos enviá-la para algum posto dos correios para que seja entregue. Evidentemente, é conveniente que os carteiros não precisem andar muito para entregar as cartas, portanto, a nossa carta deve ser enviada ao posto mais próximo do endereço destino.
O problema então é o seguinte: dados n pontos no plano, 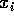 , com
, com 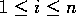 ,
e um ponto destino p, dizer qual o ponto
,
e um ponto destino p, dizer qual o ponto 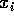 mais próximo de p.
mais próximo de p.
Uma forma direta e ingênua de atacar o problema é usar a força bruta. Calculamos
todas as distâncias 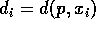 , do ponto p ao ponto
, do ponto p ao ponto 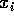 , e procuramos a menor.
Esta forma funciona, mas vamos complicar um pouco. E se quisermos resolver este problema
para muitas cartas? Será que não podemos fazer melhor?
, e procuramos a menor.
Esta forma funciona, mas vamos complicar um pouco. E se quisermos resolver este problema
para muitas cartas? Será que não podemos fazer melhor?
Como os n pontos 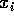 são fixos, podemos organizá-los previamente, para que não
seja necessário calcularmos todas as distâncias a cada carta.
O ideal seria se conseguissemos guardar em cada ponto do plano a
informação de qual o ponto mais próximo. Como o plano é
infinito e contí nuo, isto é impossí vel!
são fixos, podemos organizá-los previamente, para que não
seja necessário calcularmos todas as distâncias a cada carta.
O ideal seria se conseguissemos guardar em cada ponto do plano a
informação de qual o ponto mais próximo. Como o plano é
infinito e contí nuo, isto é impossí vel!
E se limitarmos o plano? Sim, podemos limitar o plano, já que na prática teremos limites. Limites de paí ses, por exemplo. Mesmo assim o número de pontos continua infinito. Só nos resta dividir o plano em um número finito de regiões, para as quais possamos achar o ponto mais próximo de forma rápida.
Podemos observar que em torno de cada ponto 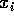 existe uma região
existe uma região 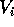 onde qualquer ponto
onde qualquer ponto 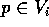 tem como ponto mais próximo o ponto
tem como ponto mais próximo o ponto 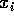 .
A divisão do plano nestas regiões tem o nome de Diagrama de Voronoi
que veremos na seção 3.3.
.
A divisão do plano nestas regiões tem o nome de Diagrama de Voronoi
que veremos na seção 3.3.
Calcular estas regiões e saber em qual delas está o ponto p não são tarefas fáceis, mas é uma opção!
Que tal uma idéia mais simples? Vamos dividir a região do plano em pequenos retângulos iguais. Saber em qual retângulo está o ponto p é bastante simples (ver figura 2.3). Você consegue descobrir como?
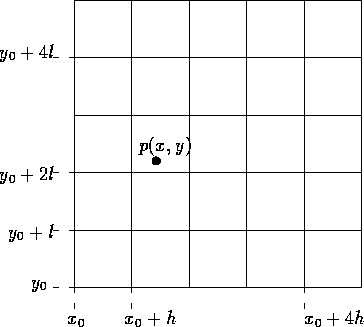
Figure: Subdivisão em retângulos de lados l e h
E para saber qual o ponto mais próximo de p? Se, para cada retângulo, guardarmos uma lista de todos os possí veis pontos, é só usar o algoritmo inicial (força bruta) com os pontos da lista do retângulo onde está p.
Falta ainda saber como escolher os pontos para as listas. Todos os pontos
que estão no retângulo R devem pertencer à lista 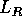 do
retângulo R. Como um ponto x pode estar em um dos vértices, e o
ponto p no outro, qualquer ponto, mesmo fora do retângulo, que esteja
a uma distância menor ou igual à distância entre x e p deve estar
na lista. Ou seja, qualquer ponto que esteja a uma distância menor ou
igual a diagonal do retângulo,
do
retângulo R. Como um ponto x pode estar em um dos vértices, e o
ponto p no outro, qualquer ponto, mesmo fora do retângulo, que esteja
a uma distância menor ou igual à distância entre x e p deve estar
na lista. Ou seja, qualquer ponto que esteja a uma distância menor ou
igual a diagonal do retângulo, 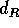 , de qualquer ponto do retângulo
R deve estar na lista (veja figura 2.4). Como a região
resultante não é simples, escolheremos o menor cí rculo que englobe
esta região, que será o cí rculo de raio
, de qualquer ponto do retângulo
R deve estar na lista (veja figura 2.4). Como a região
resultante não é simples, escolheremos o menor cí rculo que englobe
esta região, que será o cí rculo de raio 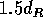 centrado no centro
centrado no centro
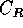 do retângulo R. Chamaremos esta região de
do retângulo R. Chamaremos esta região de 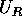 .
.
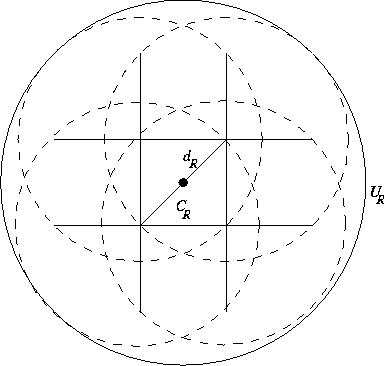
Figure: Região de pontos próximos
Caso não existam pontos na região 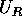 , colocaremos na lista
, colocaremos na lista 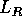 o ponto mais próximo do centro
o ponto mais próximo do centro 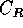 .
.
O pré-processamento, ou seja, a geração da malha e das listas 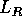 ,
demora um tempo
,
demora um tempo 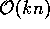 , onde k é o número de retângulos,
e a estrutura de dados (listas
, onde k é o número de retângulos,
e a estrutura de dados (listas 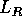 ) ocupam um espaço
) ocupam um espaço 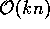 também. Mas se os retângulos tiverem a proporção dos lados
dentro de um certo intervalo,
então cada ponto
também. Mas se os retângulos tiverem a proporção dos lados
dentro de um certo intervalo,
então cada ponto 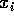 aparece no máximo em um número constante S de
listas (
aparece no máximo em um número constante S de
listas ( 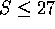 se o menor lado não é menor que a metade do maior).
Isto faz com que o espaço seja
se o menor lado não é menor que a metade do maior).
Isto faz com que o espaço seja 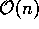 .
.
O algoritmo então fica da seguinte forma:
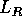 , e o ponto p.
, e o ponto p.
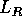 e ache
o mais próximo, x.
e ache
o mais próximo, x.
Este algoritmo tem complexidade de pior caso igual a do algoritmo inicial,
mas como o número de pontos em cada lista 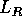 é bem menor que n
(na média n S / k, onde S é a constante mencionada acima), o algoritmo
se torna mais eficiente com o aumento do número de retângulos.
é bem menor que n
(na média n S / k, onde S é a constante mencionada acima), o algoritmo
se torna mais eficiente com o aumento do número de retângulos.