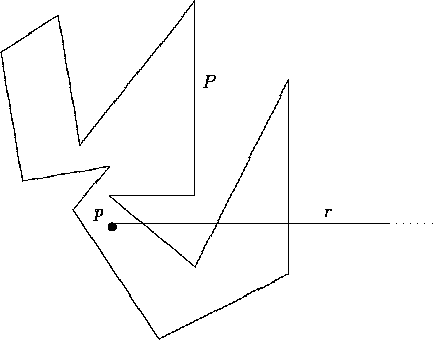
Figure 2.1: Semireta
Um problema bastante conhecido é o de saber se um determinado ponto p está no interior de um certo polí gono plano simples P.
Usando o fato de que um polí gono simples é uma Curva de Jordan, e por isso divide o plano em duas regiões conexas e abertas, podemos construir um algoritmo que utilize uma semi-reta partindo de p. Esta semi-reta estará alternadamente dentro e fora do polí gono em questão, mudando de estado nos pontos de intersecção com a borda (ver figura 2.1). Se o número de intersecções for impar, o ponto está dentro, se for par, está fora.
Para calcularmos o número de intersecções de uma semi-reta r (digamos, horizontal para a direita de p) com o polí gono P, precisaremos calcular sua intersecção com cada uma das arestas de P. Percebam que, se a semi-reta r passar por um dos vértices de P, teremos a contagem alterada (ver figura 2.2).
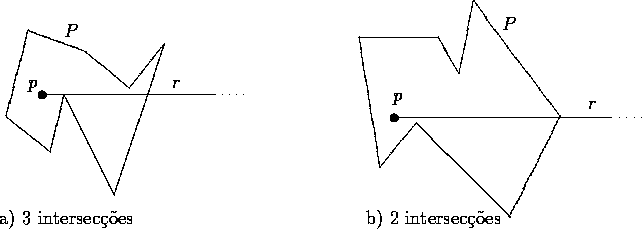
Figure: Casos de intersecção nos vertices
Aqui temos duas opções para resolver o problema. Uma é escolher qualquer outra semi-reta, por exemplo, girando a semi-reta r poucos graus. Quando nenhum dos vértices pertencer a semi-reta, efetuar o cálculo das intersecções. Esta opção tem a desvantagem de ser preciso verificar se os vértices pertencem a semi-reta.
A outra opção é tratarmos de forma diferenciada as intersecções nos vértices. Nos casos em que o vértice é máximo (ou mí nimo) local (ver figura 2.2 (a)), a semi-reta não entra nem sai do polí gono, portanto, para que a contagem fique certa, o número de intersecções deve ser par. Nos demais casos a semi-reta realmente entra ou sai do polí gono, e o número de intersecções\ deve ser í mpar (ver figura 2.2 (b)).
Se considerarmos cada aresta como sendo um segmento de reta aberto no extremo inferior e fechado no extremo superior, o número de intersecções nos vértices máximos locais será 2 (dois), que é par, nos mí nimos locais será 0 (zero), que podemos considerar como par para os nossos propósitos, e 1 (um) nos demais casos.
Observem também que temos que descartar as arestas horizontais. Tente descobrir o motivo!
Calcular a intersecção de uma semi-reta com um segmento de reta é uma operação\
simples, que pode ser feita em tempo constante. Sendo assim, supondo que o polí gono P
tem n arestas, temos que calcular n intersecções, portanto, nosso pequeno algoritmo
tem complexidade 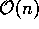 no pior caso.
no pior caso.