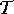Triangulação

 

Outra forma de organizar pontos, é definir sobre eles uma relação de vizinhança, ou seja, ligar pontos segundo algum critério de forma a estabelecer uma subdivisão do espaço que ocupam.

Uma destas organizações é a triangulação, que, embora o nome sugira, não se limita a dividir o plano em triângulos, mas qualquer espaço em simplexos.

Simplexos são extensões de triângulos em outras dimensões, como segmentos de reta, tetraedros, e etc. Chamamos de faces de um simplexo, todos os subsimplexos que o formam, como os vértices e arestas de um triângulo.

Mais uma vez vamos nos limitar ao plano, para não complicar muito, já que o objetivo não é esse.

Uma triangulação 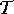é um conjunto de simplexos tais que:

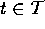• Todas as faces de também pertencem a ;
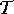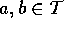• se e 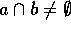então existe 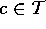tal que .

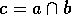Assim, a figura 2.8 (a) apresenta uma triangulação, enquanto que na figura 2.8 (b) a segunda propriedade não é satisfeita.

  
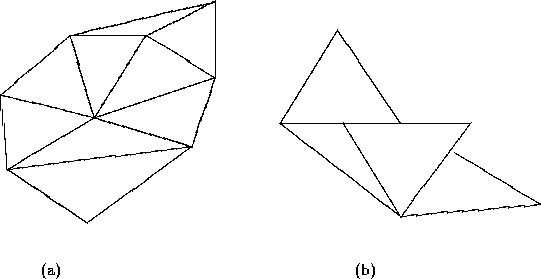
Figure: a) Exemplo de triangulação, b) coleção qualquer

Uma triangulação qualquer nem sempre é adequada para um certo problema. Para a maior parte dos algoritmos que precisam de triangulações, os triângulos precisam ser ``gordinhos'', parecidos com o triângulo equilátero. Essas triângulações especiais usam critérios de ``gordura'' para seus triângulos. Uma destas é a triangulação de Delaunay, que usa o seguinte critério:

Um certo triângulo t faz parte da triangulação de Delaunay somente se o cí rculo formado pelos vértices do triângulo não contém nenhum outro vértice de em seu interior.

Na verdade este critério é fraco, pois podem existir 4 vértices co-circulares, a, b, c e d, sendo que não existam outros pontos no interior do cí rculo, o que faria com que os 4 triângulos, abc, abd, acd e bcd, satisfizessem o critério, mas somente 2 deles poderiam fazer parte da triângulação. Isso faz com que a triangulação de Delaunay não seja única.

Se assumirmos que o conjunto de pontos não contém 4 pontos na situação acima, podemos garantir que a triangulação é única, e o critério, além de condição\ necessária, passa a ser também uma condição suficiente.

Na figura 2.9 vemos ilustrado o critério acima, e podemos observar que, se uma certa aresta atrapalha o critério, podemos trocá-la por outra.

  
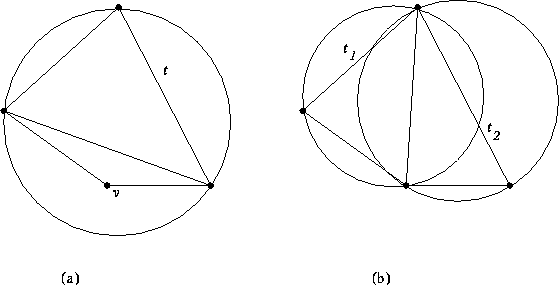
Figure 2.9: Critério de Delaunay

Podemos reescrever este critério com relação às arestas, e terí amos o seguinte teorema:

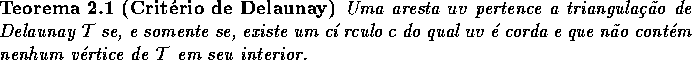
Prova: necessidade é trivial:

Seja 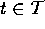um triângulo. Suas 3 arestas estão em 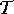. O cí rculo que passa pelos seus vértices tem suas arestas como cordas e não possui nenhum vértice em seu interior.

Agora a suficiência:

Suponha que uv seja tal que existe um cí rculo c como no enunciado do teorema. Posso escolher c de forma que seja maximal, ou seja, aumentar o seu raio faria com que algum ponto passasse a fazer parte de seu interior. Existem no máximo 2 e no mí nimo 1 cí rculo nessa situação (veja figura 2.10). Escolha c de forma que o raio seja o menor entre os maximais. Como c é maximal, existe um vértice, w, na fronteira de c. Então c passa por 3 vértices de 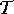e não contém nenhum outro vértice em seu interior, logo o triângulo uvw faz parte de 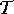, e consequentemente suas 3 arestas também.

  
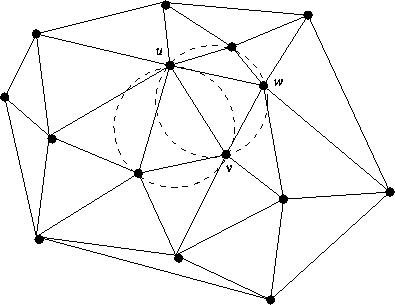
Figure: 2 cí rculos maximais da aresta uv

Este critério sugere um algoritmo simples, a partir de uma triangulação qualquer, procurar as arestas que atrapalham o critério e trocá-las por suas opostas, como na figura 2.9. Certamente este algoritmo termina, já que ao trocar uma aresta nos aproximamos da triangulação de Delaunay. Mas não é muito eficiente.

Que tal um algoritmo incremental? Partindo de uma triangulação inicial, com 3 vértices não necessariamente no conjunto, mas que formem um triângulo que envolva todos os outros, incluir os vértices um a um, descobrindo em qual triângulo eles estão, subdividindo este triângulo em três, como mostra a figura 2.11, e atualizando a triangulação. As três novas arestas respeitam o critério de Delaunay (veja [GS85]), mas as arestas vizinhas não se sabe. Como elas podem ser trocadas, é preciso que o processo seja expandido até que todos estejam em ordem.

  
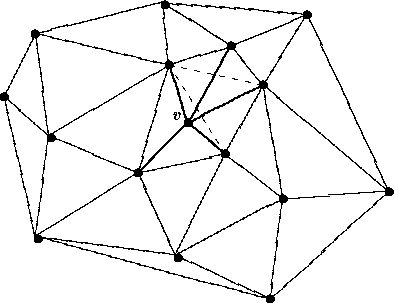
Figure: Divisão de um triângulo em 3

Esta expansão não vai muito longe na prática, pelo seguinte argumento: para as arestas estarem erradas, é preciso que o novo ponto esteja razoavelmente próximo delas para que atrapalhe o critério de Delaunay, já que nenhum outro ponto atrapalhava até o momento. Outro detalhe importante é o fato de que todas as arestas novas são incidentes ao novo ponto (veja [GS85, lema 7.4,]).

No pior caso este algoritmo tem complexidade 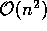, porém é considerado um bom algoritmo.